- Instituto de Estadística, Departamento de Métodos Cuantitativos, Facultad de Ciencias Económicas y de Administración, Universidad de la República.
RESUMEN
Palabras clave: Deuda soberana; curva de rendimiento; modelos estáticos; modelos dinámicos.
ABSTRACT
Keywords: Sovereign debt; term structure; static models; dynamic models.
JEL Code: C01, C23, C51, E43, E44, H63
INTRODUCCIÓN
La deuda soberana es el conjunto de la deuda pública que mantiene con respecto a sus acreedores. Esta deuda principalmente se genera a través de la emisión de activos de renta fija en los mercados financieros.
Al analizar el comportamiento de los precios de sus activos se percibe que la evolución temporal en sus tasas de rendimient depende de una gran cantidad de variables. Estas variables inciden tanto en el mercado primario al emitirse el activo como en el mercado secundario al ser transados por agentes financieros. En la demanda de esta clase de activos influye el nivel crediticio del emisor, la liquidez que presentan los activos, el tipo de cambio del país emisor y las tasas de interés esperadas, en otras posibles inversiones. En cuanto a la oferta de activos soberanos se destaca las necesidades financieras del estado emisor, las oportunidades de costos y beneficios en el momento de emisión y el valor esperado de diversas variables macroeconómicas como lo pueden ser la tasa de inflación y el tipo de cambio.
En la composición de la deuda soberana existe una gran cantidad de activos financieros que se diferencian entre sí por diversas razones. Para el objetivo del trabajo, es necesario resaltar esencialmente el vencimiento del activo financiero y la moneda de emisión. Esto se debe a que entre los activos que presentan el mismo riesgo crediticio, misma liquidez y mismas características en las condiciones del contrato, pero se diferencian en sus vencimientos las tasas de rendimientos inducidas son distintas.
Se establece que la curva de rendimiento (term structure) en una determinada moneda es la función que relaciona las tasas de rendimiento con los vencimientos en los activos financieros. En este caso, se entiende que la tasa de rendimiento es aquella tasa de interés que iguala el precio transado del activo con su valor presente del flujo futuro de pagos.
La utilidad de conocer la curva de rendimiento presenta varias perspectivas. Desde el análisis macroeconómico, las autoridades monetarias extraen información sobre las expectativas de tasas de interés y tasas de inflación futuras del mercado con el fin de planificar políticas públicas. Desde el análisis financiero existen diferentes alternativas, entre ellas se destacan los estudios de sensibilidad en activos dentro de un portafolio de renta fija y la valuación de otros activos como son los derivados financieros. Existe evidencia empírica en que existe relación entre la fijación de los precios de los diferentes activos y la eficiencia que presenta dicho mercado financiero. Esto se debe que a criterios adecuados en la valuación de los activos permiten comprender de mejor manera sus riesgos asociados.
La propuesta del trabajo se basa en realizar un análisis profundo de algunos modelos y métodos de estimación de curvas de rendimiento, con énfasis en el mercado de Uruguay. En la sección 1, se establece la importancia económica en el problema de valuación de la deuda soberana. En la sección 2, se establecen los principales modelos y métodos utilizados en el mercado en Uruguay mediante el enfoque estático. Se realizan estimaciones de los modelos y se analiza una situación real en el mercado uruguayo. Este análisis permite observar las posibles desventajas que presenta el enfoque estático en Uruguay. En la sección 3 se realiza una breve reseña de la literatura del enfoque dinámico en la valuación de curvas de rendimiento. Se selecciona una clase de modelos denominados Gaussian Affine Term Structure Model y se realizan estimaciones diarias de las curvas de rendimiento de la deuda soberana nominada en dólares durante tres años. En la sección 4, se establecen las conclusiones del trabajo.
ENFOQUE ESTÁTICO
La curva de rendimiento es una función de las tasas de interés con respecto a sus vencimientos que se observa de manera empírica sólo en ciertos tiempos futuros. En las últimas décadas, la profundización en los modelos matemáticos teóricos y los métodos de estimación al utilizar la información disponible en el mercado se transformó en un área de desarrollo tanto en ámbitos académicos como en los agentes financieros participantes de los mercados.
La pregunta natural es, si existen modelos que presentan mejores propiedades específicas con respecto a los demás. La respuesta general es que no existen tales modelos al ser dependientes de su utilidad y de la naturaleza de los datos utilizados en la estimación. Sin embargo, existen características que pueden mejorar los resultados bajo ciertas circunstancias, entre ellos se destacan la flexibilidad en el rango de curvas que alcanza y la suavidad de las curvas generadas principalmente en los vencimientos de largo plazo. Esta situación presenta como consecuencia que, si bien los agentes financieros tienen sus propios modelos de referencia para el análisis, se encuentran interesados en la investigación en estos temas.
Selección de modelos
Al seleccionar el modelo para utilizar en la estimación de las curvas de rendimiento es posible establecer ciertos objetivos deseados. Entre ellos se destaca la necesidad de que la curva de rendimiento estimada replique exactamente los precios transados en el mercado. Por ejemplo, esta característica es requerida en el contexto de valuación de portafolios, pero en varias situaciones su costo negativo es la forma irregular e inestable de la estimación.
La perspectiva más utilizada en los mercados financieros es la estimación estática en la cual se analiza de manera transversal a todos los activos transados en un determinado momento. Es decir, no se explora la dimensión temporal en las tasas de rendimiento. Dentro de todos los modelos estáticos existen diferentes enfoques para abordar el problema. Una manera de clasificar a los modelos son modelos paramétricos y modelos no paramétricos.
Modelos utilizados en el mercado financiero en Uruguay
En una exploración del mercado uruguayo, las bolsas de valores en Uruguay --Bolsa Electrónica de Valores Sociedad Anónima (BEVSA) y Bolsa de Valores de Montevideo (BVM)— publican estimaciones diarias de curvas de rendimiento del mercado (en algunas monedas). Cada institución, presenta un informe técnico en el cual se establecen las metodologías de estimación y los criterios que se emplean en la construcción de las curvas de rendimiento. También existe una metodología implementada en el Banco Central del Uruguay (BCU), que si bien no se comporta como una habitual curva de rendimiento, es un criterio de fijación de todos los precios de activos emitidos por el estado uruguayo. Estos precios se publican de manera diaria y presentan una vital importancia en el mercado financiero uruguayo debido a que las Administradoras de Ahorro Previsional (AFAP) y las empresas de Seguros y Reaseguros se encuentran obligadas a utilizar tales precios para la valuación contable de los activos que forman parte de sus portafolios de inversión.
En el caso de la BEVSA se publican a diario las curvas de rendimientos en las tres principales monedas de emisión de la deuda soberana en Uruguay (dólares, unidades indexadas y pesos uruguayos). El documento explicativo sobre el modelo, el método de estimación y los datos a utilizar se encuentra en (Mara, 2017). En el caso de la BVM, se publica únicamente la curva de rendimiento diaria en unidades indexadas. El enfoque de estimación que utiliza es la metodología mediante funciones. Para finalizar, el BCU publica de manera diaria los precios de todos los activos que circulan en el mercado en el denominado Vector de Precios. Por más información ver (BCU).
Descripción de los modelos
En esta sección se analizan las dos principales metodologías utilizadas en Uruguay con el fin de comprender sus fundamentos. Es importante destacar que la teoría matemática se desarrolla en el entorno habitual de cada uno de los modelos.
Métodos de estimación mediante splines
El método de estimación general mediante spline se basa en encontrar una función desconocida desde un conjunto de
![]() coordenadas
coordenadas ![]() (puntos vértices) con sus correspondientes valores
(puntos vértices) con sus correspondientes valores ![]() al imponer ciertas restricciones de suavidad en el intervalo
al imponer ciertas restricciones de suavidad en el intervalo ![]() En el análisis, la función
En el análisis, la función ![]() es la correspondiente al descuento del mercado, es decir, el precio de un bono cupón cero en todos los vencimientos.
es la correspondiente al descuento del mercado, es decir, el precio de un bono cupón cero en todos los vencimientos.
De manera general, la propuesta es ajustar uno o varios polinomios que cumplan ciertas características relacionadas a los datos. En el caso que se requiera que la estimación deba coincidir con los datos, esta metodología une los valores mediante polinomios de grado ![]() (
(![]() lineales,
lineales, ![]() cuadráticos,
cuadráticos, ![]() cúbicos, entre otros). De acuerdo a la cantidad de parámetros establecidos en la función, es necesario agregar ciertas condiciones, que pretenden suavizar las funciones en los puntos vértices. Si se considera un conjunto grande de datos, el número de parámetros a estimar es excesivo, por lo cual con el fin de reducir dicho número se desarrolla la metodología denominada B-splines cúbicos. En este método se fija con anterioridad una base de polinomios de grado 3 y se establece que la función
cúbicos, entre otros). De acuerdo a la cantidad de parámetros establecidos en la función, es necesario agregar ciertas condiciones, que pretenden suavizar las funciones en los puntos vértices. Si se considera un conjunto grande de datos, el número de parámetros a estimar es excesivo, por lo cual con el fin de reducir dicho número se desarrolla la metodología denominada B-splines cúbicos. En este método se fija con anterioridad una base de polinomios de grado 3 y se establece que la función ![]() es una combinación lineal entre los polinomios. Se consideran
es una combinación lineal entre los polinomios. Se consideran ![]() puntos diferentes
puntos diferentes ![]() en el período de tiempo de análisis y se agregan tres puntos más antes del inicio
en el período de tiempo de análisis y se agregan tres puntos más antes del inicio ![]() y tres puntos más después del final
y tres puntos más después del final ![]() Los
Los ![]() polinomios que forman parte de la base B-spline son las funciones
polinomios que forman parte de la base B-spline son las funciones ![]() en el intervalo
en el intervalo ![]() dadas mediante
dadas mediante
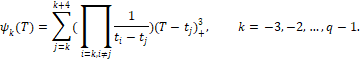
El elemento ![]() de la base de B-splines es un polinomio cúbico que toma valores estrictamente positivos en el intervalo
de la base de B-splines es un polinomio cúbico que toma valores estrictamente positivos en el intervalo ![]() y es cero fuera de él. En cada valor de
y es cero fuera de él. En cada valor de ![]() del dominio
del dominio ![]() existen sólo cuatro polinomios diferentes de cero. Por más detalles en el método de B-spline cúbicos, ver (Filipovic, 2009) y (Jamieson y Scott, 2002). La curva de descuento del mercado se establece mediante una combinación lineal de las funciones de la base, es decir
existen sólo cuatro polinomios diferentes de cero. Por más detalles en el método de B-spline cúbicos, ver (Filipovic, 2009) y (Jamieson y Scott, 2002). La curva de descuento del mercado se establece mediante una combinación lineal de las funciones de la base, es decir
![]()
Si se denota a ![]() como el vector de precios del mercado de los
como el vector de precios del mercado de los ![]() activos que se utilizan en la estimación; a
activos que se utilizan en la estimación; a ![]() como la matriz de dimensión
como la matriz de dimensión ![]() (
(![]() es la cantidad total de tiempos de pagos entre todos los activos) en la cual la fila
es la cantidad total de tiempos de pagos entre todos los activos) en la cual la fila ![]() establece los flujos de fondos del activo
establece los flujos de fondos del activo ![]() ; a
; a ![]() como la matriz de dimensión
como la matriz de dimensión ![]() (
(![]() ) donde la columna
) donde la columna ![]() es la función
es la función ![]() evaluada en cada tiempo y a
evaluada en cada tiempo y a ![]() como el vector de dimensión
como el vector de dimensión ![]() de parámetros del modelo. El problema estadístico que resulta es estimar los parámetros mediante la optimización
de parámetros del modelo. El problema estadístico que resulta es estimar los parámetros mediante la optimización
![]()
Métodos de estimación mediante funciones
La segunda metodología considera el ajuste de la función desconocida a curvas paramétricas predeterminadas. Estos modelos no utilizan varios polinomios para el ajuste, sino que existe una única función definida en todos los vencimientos. Las dos ventajas que presentan estos modelos frente a los modelos de splines es la menor cantidad de parámetros involucrados en la estimación y la suavidad de la curva de rendimientos que se obtiene. El desarrollo de estos modelos se realiza en la tasa de interés forward, la cual es la tasa de interés que genera una inversión en tiempo futuro con horizonte temporal que tiende a cero.
La diferencia entre los modelos de este método es la selección de la función. En esta subsección se desarrollan los dos modelos más utilizados en la estimación de curvas de rendimiento mediante este enfoque. La estimación de los parámetros se realiza mediante la minimización de diferencia entre las tasas de interés del mercado y las tasas de interés del modelo, que se ejecuta a través de algoritmos de optimización no lineales.
En el trabajo (Nelson y Sieger, 1987), los autores asumen que la forma de la función de la tasa de interés forward ![]() en el momento
en el momento ![]() para tiempo
para tiempo ![]() es dada mediante
es dada mediante
![]()
donde los parámetros ![]() ,
, ![]() ,
, ![]() y
y ![]() son coeficientes que cumplen
son coeficientes que cumplen ![]() .
.
La función que se determina mediante la ecuación (1) es capaz de capturar una variada gama de formas de curvas de rendimiento que se observan en el mercado. Esto se debe a que la función ![]() consta de tres sumandos en el cual cada uno aporta diferentes características. El primer sumando es una función constante que tiene su mayor importancia en el largo plazo; el segundo sumando es una función exponencial decreciente que tiene importancia en la pendiente de la función y el tercer sumando es una función positiva que comienza en cero, tiene límite cero en infinito y que presenta un único máximo el cual tiene importancia en la curvatura.
consta de tres sumandos en el cual cada uno aporta diferentes características. El primer sumando es una función constante que tiene su mayor importancia en el largo plazo; el segundo sumando es una función exponencial decreciente que tiene importancia en la pendiente de la función y el tercer sumando es una función positiva que comienza en cero, tiene límite cero en infinito y que presenta un único máximo el cual tiene importancia en la curvatura.
Desde la existencia de este modelo, varios otros han sido propuestos al incorporar mayor flexibilidad. La extensión más popular es el modelo propuesto por Lars Svensson en el trabajo (Svensson, 1994) bajo el costo de agregar dos parámetros más al modelo. En el modelo propuesto, a la ecuación (1) se le agrega un sumando responsable de permitir otro punto de inflexión adicional. Es decir,
![]()
donde los parámetros ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() son coeficientes que cumplen
son coeficientes que cumplen ![]() y
y ![]() .
.
A causa de la gran flexibilidad que presentan las funciones exponenciales el modelo tiene como consecuencia la posibilidad de obtener resultados de curvas monótonas crecientes, decrecientes, formas de U y formas de S.
Situación empírica en el mercado en Uruguay
Con el fin de analizar las curvas de rendimiento publicadas en el mercado uruguayo y las tasas de rendimiento inducidas por el Vector de Precios publicado por el BCU, se considera el caso de la deuda soberana nominada en unidades indexadas el día viernes 09 de marzo de 2018. En este día, existían en circulación 5 bonos globales con vencimiento entre los años 2018 y 2037 y 11 notas de tesorería con vencimiento entre los años 2018 y 2030. Sin embargo, en el mercado local se transaron cuatro bonos globales de vencimientos en los años 2018, 2027, 2028 y 2037 y la nota de tesorería serie 19 (vencimiento en el año 2022).
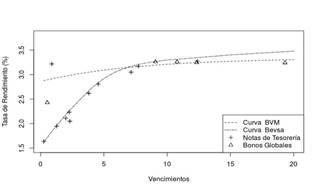
En la Figura 1, se encuentran (aproximaciones) de las curvas de rendimiento publicadas en ambas bolsas de valores y las tasas de rendimiento derivadas de los precios de los activos publicados en el BCU. Se observa gran disparidad entre las dos curvas de rendimientos publicadas.
Figura 1: Información publicada en el mercado uruguayo por distintos agentes el viernes 09 de marzo de 2018
Estimación de los modelos
En el trabajo se propone implementar el método de B-spline, el método de Nelson-Siegler y el método de Svensson con el fin de comparar los resultados con la información publicada en el mercado.
Se realizan tres estimaciones de los modelos planteados con diferente cantidad de información disponible del día 09 de marzo de 2019. En todas las estimaciones se utiliza el precio de los cinco activos financieros transados en el mercado y se adicionan otros activos de acuerdo a ciertas estrategias con el fin de analizar los cambios en la estructura de las curvas estimadas. En el primer caso, se agregan las cuatro notas de tesorería que presentan mayor circulante. En el segundo caso, se agrega el bono global de vencimiento en el año 2030 y las cuatro notas de tesorería que generan la mejor distribución en los vencimientos de los activos utilizados. En el tercer caso, se utilizan todos los activos financieros en circulación. Las curvas de rendimiento en cada estimación se encuentran en la Figura 2 y los parámetros asociados a las estimaciones mediante funciones se encuentran en el Cuadro 1.
Figura 2: Estimaciones de curvas de rendimiento en modelos estáticos para el día 09/03/2018
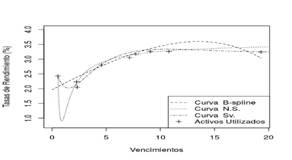
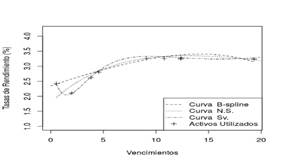
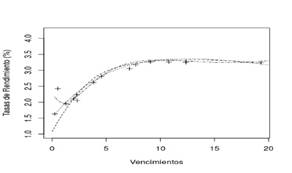
Tabla 1: Estimación de parámetros en los modelos de Nelson-Siegel y Svensson
N.S. 1 |
Sv. 1 |
N.S. 2 |
Sv. 2 |
N.S. 3 |
Sv. 3 |
|
|
3.572 |
7.251 |
0.046 |
11.564 |
0.673 |
14.067 |
|
35.793 |
-3.981 |
1.738 |
-8.353 |
0.835 |
-11.751 |
|
-50.421 |
-8.595 |
8.124 |
-11.631 |
7.662 |
-10.501 |
|
0.213 |
1.213 |
9.613 |
1.413 |
8.013 |
1.813 |
|
--- |
-11.322 |
--- |
-23.171 |
--- |
-29.836 |
|
--- |
15.613 |
--- |
13.013 |
--- |
13.813 |
Es posible concluir que en los modelos utilizados se obtienen estructuras de curvas de rendimiento que dependen fuertemente de los activos utilizados. A su vez en el caso de las metodologías vía funciones, los valores en los parámetros presentan mucha variabilidad. Esta característica hace muy difícil asociar el comportamiento de la curva de rendimiento a la interpretación teórica de cada parámetro que se establece en la subsección 2.3. Como aspecto a destacar es importante establecer que las estructuras en las curvas de rendimiento se conservan tanto en el modelo de B-spline como en el modelo de Svensson.
Valoración de los modelos
En la literatura existen consensos en que son los modelos más utilizados en los mercados financieros y que presentan una gran cantidad de aspectos positivos. Sin embargo, en sintonía a las conclusiones que se obtienen en el análisis anterior, también existen algunas críticas a los modelos que se enfocan principalmente en ciertos análisis empíricos. Las críticas se basan en ciertas propiedades no deseadas, entre las que se destacan el ajuste a los precios de mercado, la adecuación a los activos utilizados y la perspectiva teórica de la economía.
Una crítica general es el compromiso entre cantidad de parámetros en los modelos y cantidad de datos a utilizar en la estimación. Esta situación presenta relevancia principalmente en mercados financieros ilíquidos. Esto se debe, a que si únicamente se utilizan activos financieros transados en el mercado en varias ocasiones es posible que no se transen la cantidad suficiente de activos como para estimar de manera robusta los parámetros del modelo, ejemplo ver (Orsag y Zoricic, 2013). A este aspecto, se adicional que en el caso de poca información es posible que las estimaciones de las curvas de rendimiento sean muy volátiles al ingreso de nueva información. Entre otras referencias se encuentra (Xie et al., 2006).
Con respecto al método de estimación vía B-spline, la principal crítica radica en la dependencia en la cantidad de polinomios de la base y en la ubicación de los nodos de la base. Si bien existen metodologías que establecen candidatos a nodos a seleccionar, entre ellos (Dung y Tjahjowidodo, 2017), en caso que no se establezca o se disponga de la información certera, es posible que este método sea considerado ``modelos de caja negra"", al no poder replicar los resultados exactos. Con respecto al método de Nelson y Siegel o Svensson, existen varios trabajos que apuntan a críticas sobre las estimaciones en algunas situaciones empíricas, principalmente se centran en el problema de multicolinealidad al estimar el modelo. En varios trabajos se proponen modificaciones a la forma funcional de la curva de tasa de interés forward con el fin de adecuarse a la liquidez presente en el mercado, ejemplo ver (Dutta et al., 2005).
ENFOQUE DINÁMICO
En la actualidad, existe una gran preocupación en la investigación en esta área por estudiar modelos y métodos de curvas de rendimiento en mercados ilíquidos. Los problemas usuales de poca información disponibles para realizar la estimación se traducen en obtener una matriz esparza en la matriz de precios de activos, el cual es un área de investigación importante de análisis numérico.
Desde nuestra visión, el problema de estimación de curvas de rendimiento en el Uruguay es posible abordarlo desde el punto de vista dinámico. Existen desarrollos teóricos que intentan captar el comportamiento dinámico de las tasas de interés desde diferentes enfoques. El objetivo general es establecer modelos que incluyan ciertos procesos estocásticos (en tiempo discreto o continuo) que tiendan a representar la evolución de las diferentes tasas de rendimiento respecto al vencimiento.
El análisis implica el estudio de series de tiempo de ciertos activos soberanos en contraposición a los modelos estáticos en los cuales sólo se consideran de manera transversal. Se pretende que las estimaciones de las curvas de rendimiento no dependan en gran medida de los activos transados en un día en un momento de tiempo al incrementar de manera notoria la cantidad de información que se utiliza.
La teoría de la modelación dinámica en tasas de interés creció de manera exponencial al adecuarse a los nuevos activos que se desarrollan en el mercado. De breve manera, es posible establecer que existen principalmente tres metodologías de modelación que presentan características diferentes y utilizan distintas clases de datos del mercado para su estimación. Sin embargo, debido a la naturaleza de los activos disponibles en la deuda soberana en Uruguay desde nuestra opinión es posible aplicar la metodología de los modelos de tasa de interés spot instantánea (short rate models). La literatura académica es muy variada, algunos libros de referencia son (Bjork, 2009), (Brigo y Mercurio, 2006), y (Musiela y Rutkowski, 2005). En lo que refiere a los métodos de estimación, estos se complejizan al implicar el estudio de algunas series de tiempo. Existen una gran diversidad de artículos científicos que proponen nuevos métodos de estimación; en el libro (Harvey, 1992) se encuentra la base matemática para varios de estos métodos.
Modelo Econométrico
En el trabajo, se propone utilizar los modelos dinámicos gaussianos denominados Gaussian Affine Term Structure model (GATS) que especifican que la tasa de interés instantánea (short rate) es una función determinista de un vector de estados ![]() dimensional que satisface una ecuación diferencial estocástica que depende de un movimiento browniano multidimensional. La selección de esta clase de modelos se basa en el compromiso entre generalidad y tratabilidad, esto se debe a que la fórmula de la tasa de rendimiento del bono soberano es una función lineal de los vectores de estado. Por esta característica, estos modelos son muy utilizados en la literatura.
dimensional que satisface una ecuación diferencial estocástica que depende de un movimiento browniano multidimensional. La selección de esta clase de modelos se basa en el compromiso entre generalidad y tratabilidad, esto se debe a que la fórmula de la tasa de rendimiento del bono soberano es una función lineal de los vectores de estado. Por esta característica, estos modelos son muy utilizados en la literatura.
La dinámica del vector de estados latentes es dada
![]()
donde ![]() es un vector
es un vector ![]() ,
, ![]() y
y ![]() son matrices
son matrices ![]() , y
, y ![]() es un movimiento browniano
es un movimiento browniano ![]() -dimensional definido en un espacio de probabilidad adecuado
-dimensional definido en un espacio de probabilidad adecuado ![]() . En el trabajo, se expresa
. En el trabajo, se expresa ![]() y las matrices por razón de parsimonia es elegida diagonal, por lo cual se denota
y las matrices por razón de parsimonia es elegida diagonal, por lo cual se denota ![]() y
y ![]() .
.
La ecuación 2 es una generalización del clásico modelo de Vasicek (Vasicek, 1977) por lo cual es posible realizar un procedimiento similar para la estimación de los parámetros pero de manera multidimensional. Al discretizar el proceso ![]() de
de ![]() -dimensiones al dividir el tiempo de análisis en intervalos iguales de longitud
-dimensiones al dividir el tiempo de análisis en intervalos iguales de longitud ![]() , la aproximación de Euler brinda la matriz de transición
, la aproximación de Euler brinda la matriz de transición
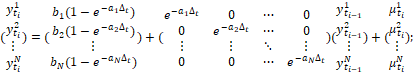 (3)
(3)
donde ![]() y
y
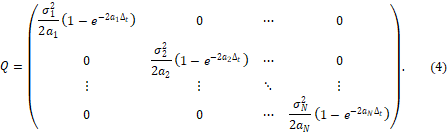
En el otro lado, al ser la generalización del modelo de Vasicek se obtiene que la tasa de rendimiento del precio del bono es una función lineal del vector de estados de la forma
![]()
donde
![]()
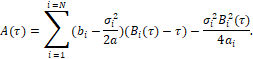
Con el fin de darle una situación más real al modelo, asumimos además que existen en el mercado ![]() bonos soberanos con vencimientos
bonos soberanos con vencimientos ![]() y respectivas tasas de rendimiento
y respectivas tasas de rendimiento ![]() , donde
, donde ![]() es el diferencial de tiempo al vencimiento. La consecuencia que tiene esta hipótesis es que puede acarrear problemas de identificación, por lo cual es necesario agregar diferencias entre las tasas de rendimiento observadas en el mercado y las tasas de rendimientos estimadas, introduciendo una variable de error
es el diferencial de tiempo al vencimiento. La consecuencia que tiene esta hipótesis es que puede acarrear problemas de identificación, por lo cual es necesario agregar diferencias entre las tasas de rendimiento observadas en el mercado y las tasas de rendimientos estimadas, introduciendo una variable de error ![]() . Este procedimiento fue introducido en (Chen y Scott, 1993) a introducir más información de bonos soberanos que dimensiones en el vector de estados. La ecuación de medida es dada
. Este procedimiento fue introducido en (Chen y Scott, 1993) a introducir más información de bonos soberanos que dimensiones en el vector de estados. La ecuación de medida es dada
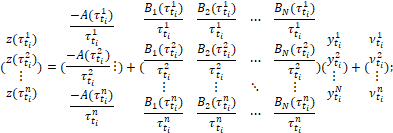
donde ![]() y
y
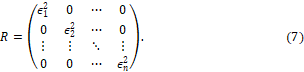
Métodos de Estimación
El problema estadístico al que nos enfrentamos es obtener los parámetros del modelo propuesto y las tasas de interés instantánea al utilizar únicamente los precios de los bonos soberanos negociados tanto en el mercado primario como en el mercado secundario. La herramienta adecuada en esta situación es el filtro de Kalman (Kalman, 1960), que se prueba que es óptimo en esta clase, ver (Harvey, 1992).
Las ecuaciones (3) y (6) forman un sistema dinámico con dos clases de informaciones: la variable no observable que describe la dinámica de la tasa de interés instantánea siguiendo un proceso de Markov; y la variable observable que corresponde a la tasa de rendimiento de los bonos soberanos. Estas dos variables se relacionan mediante una función lineal paramétrica.
El filtro de Kalman es un conjunto de ecuaciones que implementan una estimación de predictor-corrector que es actualizado al arribo de nueva información al sistema. La predicción se basa en utilizar la distribución de la variable de estado condicional al valor anterior estimado. Esta predicción se actualiza mediante la información de las tasas de rendimiento observadas en el mercado. La estimación permite construir una función de verosimilitud que permite maximizar en el conjunto de parámetros. Para la optimización, es necesario utilizar técnicas no lineales debido a su complejidad. En el trabajo, utilizamos el algoritmo denominado Expectation-Maximization (EM) que es ampliamente utilizado en varias aplicaciones, por ejemplo (Linke et al., 2014). En particular, el filtro de Kalman es utilizado para estimar curvas de tasas de rendimiento en los trabajos (Chen y Scott, 2003) y (Jamieson, 2001).
Aplicaciones al mercado en Uruguay
En esta sección se realizan estimaciones de curvas de rendimiento al mercado uruguayo en la deuda soberana nominada en dólares. Los datos que son utilizados para la modelación son los precios diarios de una serie de bonos soberanos transados en el mercado primario o en el mercado secundario en Uruguay. Los bonos seleccionados se dividen seis en bonos globales y dos en bonos locales. Estos activos abarcan una gran parte de la capitalización total de la deuda soberana emitida en dólares. Los bonos globales incluyen principalmente vencimiento de mediano y largo plazo; en cambio los bonos locales permiten tener información de los vencimientos de corto plazo. Las características de los bonos seleccionados se encuentran en la tabla 2 y el período de tiempo considerado es 04/01/2016 - 31/12/2018 (741 días hábiles).
Tabla 2: Bonos nominados en dólares utilizados en la estimación
Activo |
Emisión |
Vencimiento |
Cupón |
Bono Local 2019 |
29/03/03 |
23/03/19 |
7.500 |
Bono Local 2020 |
29/05/03 |
28/02/20 |
9.750 |
Bono Global 2022 |
18/11/05 |
18/11/22 |
8.000 |
Bono Global 2024 |
14/08/13 |
14/08/24 |
4.500 |
Bono Global 2025 |
28/09/09 |
28/09/25 |
6.875 |
Bono Global 2033 |
29/05/03 |
15/01/33 |
7.875 |
Bono Global 2036 |
21/03/06 |
21/03/36 |
7.625 |
Bono Global 2045 |
20/11/12 |
20/11/45 |
4.125 |
En el caso de los modelos de un solo factor, los resultados presentan una interpretación significativa de acuerdo a la magnitud de los parámetros estimados. La principal desventaja que soportan es que las tasas de rendimiento se encuentran perfectamente correlacionada en los vencimientos. Esta propiedad teórica del modelo no se cumple de manera empírica en las curvas de rendimiento del mercado por esta razón se mejoran los resultados al analizar modelos con mayor cantidad de factores. No obstante, al agregar factores en la modelación puede surgir el problema de sobreajuste. Para analizar esta situación existen varios criterios de información, los usuales en el problema de estimación de las curvas de rendimiento son los que se componen de dos términos: el relacionado a la bondad de ajuste en los estimadores de máxima verosimilitud y el que penaliza el número de parámetros.
En la tabla 3 se encuentran las estimaciones de los parámetros en el modelo propuesto en uno, dos y tres factores junto a las estimaciones de los errores en la ecuación (7). Además, se exhibe el valor de la función de verosimilitud y el criterio de Akaike (AIC) y el criterio bayesiano (BIC).
Tabla 3: Estimación de parámetros en el mercado en dólares
Un Factor |
Dos Factores |
Tres Factores |
|
|
0.2578 |
0.6091 |
0.6689 |
|
--- |
0.1843 |
0.2845 |
|
--- |
--- |
0.0861 |
|
0.0535 |
0.0196 |
0.0306 |
|
--- |
0.0367 |
0.0114 |
|
--- |
--- |
0.0148 |
|
0.0218 |
0.0182 |
0.0115 |
|
--- |
0.0117 |
0.0129 |
|
--- |
--- |
0.0041 |
|
0.004885 |
0.001722 |
0.001592 |
|
0.004398 |
0.001344 |
0.001256 |
|
0.003891 |
0.001291 |
0.001353 |
|
0.003595 |
0.001688 |
0.001235 |
|
0.003359 |
0.002578 |
0.001398 |
|
0.003531 |
0.002681 |
0.001272 |
|
0.003841 |
0.002755 |
0.001541 |
|
0.003866 |
0.002943 |
0.001529 |
|
3155.29 |
3339.27 |
3614.63 |
AIC |
-6288.58 |
-6650.54 |
-7195.26 |
BIC |
-6216.63 |
-6558.96 |
-7084.06 |
Para finalizar se construyen las curvas de rendimiento para todos los días analizados con el fin de observar su evolución temporal. Las curvas de rendimiento para cada modelo se encuentran en la figura 3.
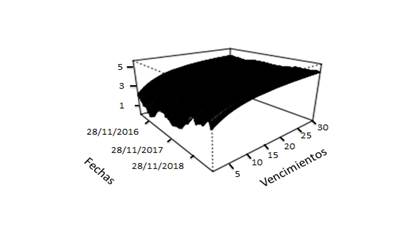
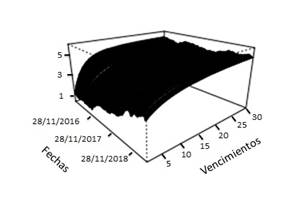
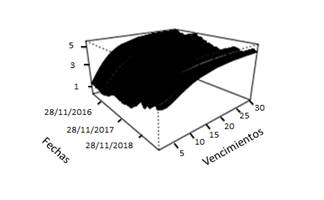
Figura 3: Curvas de rendimiento estimadas en el mercado de bonos nominados en dólares.
En las curvas de rendimiento estimadas se perciben diferencias notorias entre los modelos en un factor y los modelos en varios factores. Esto se debe a la rigidez en las estructuras de las curvas de rendimiento en los modelos de un factor, lo que provoca un ajuste adecuado en los vencimientos a corto plazo, pero no así en el largo plazo. Lo que sucede es que a mayor cantidad de dimensiones en el modelo las curvas de rendimiento producidas pueden presentar mayor cantidad de formas en la curvatura.
CONCLUSIONES
El trabajo presenta como objetivo la modelación de la deuda soberana en Uruguay a través de dos diferentes enfoques: estático y dinámico.
En el enfoque estático se analizan los dos modelos más utilizados en los mercados internacionales que coinciden con los dos modelos que aplican las bolsas de valores en Uruguay. Para estudiar el comportamiento de estos modelos, se analiza empíricamente las curvas de rendimiento publicadas por los dos agentes en el mercado en Uruguay. Se observa que existen diferencias notorias entre las curvas publicadas y se realizan distintas estimaciones al cambiar la base de datos. Se observa que las estimaciones dependen fuertemente en los bonos soberanos utilizados en la estimación. Dado que el mercado de Uruguay es poco líquido, de acuerdo a la cantidad de activos negociados de manera diaria, se convierte en un motivo para proponer otra manera de estimar la curva de rendimientos: el enfoque dinámico.
En el trabajo se exponen algunas propiedades del enfoque dinámico y se propone estudiar una clase particular de modelos debido a sus propiedades de tratabilidad. Para la estimación de los parámetros del modelo se utiliza como base la técnica del filtro de Kalman, al emplear en forma simultánea una gran cantidad de series históricas de precios de activos. Sin embargo, la función de verosimilitud que resulta no permite una maximización directa por la existencia de variables no observables. Se debe recurrir a la metodología de esperanza-maximización para la optimización. Bajo este enfoque se aplican los modelos en uno, dos y tres factores para los bonos soberanos emitidos en dólares.
Se espera que este trabajo, motive el acercamiento a la investigación del enfoque dinámico por parte de los agentes participantes del mercado con el fin de generar resultados más robustos al utilizar una mayor cantidad de datos en la estimación.
Referencias
- Banco Central del Uruguay. (BCU). https://www.bcu.gub.uy/Comunicados/seggco19114.pdf
- Bjork, T. (2009). “Arbitrage Theory in Continuous Time”. Third Edition Oxford Finance.
- Brigo, D.;Mercurio, F. (2006). ”Interest Rate Models Theory and Practice with Smile, Inflation and Credit”. Second Edition Springer Verlag.
- Chen, R.;Scott, L. (1993). ”Maximum Likelihood Estimation for a Multi Factor Equilibrium Model of the Term Structure of Interest Rates”. The Journal of Fixed Income, Vol 3, No 3, pp 14-31.
- Chen, R.;Scott, L. (2003). “Multi-Factor Cox-Ingersoll-Ross Models of the Term Structure: Estimates and Tests from a Kalman Filter Model”. The Journal of Real Estate Finance and Economics 27, pp 143-172.
- Dung, V.; Tjahjowidodo, T. (2017). “A direct method to solve optimal knots of B-spline curves: An application for non-uniform B-spline curves fitting”. PLoS ONE 12, 3.
- Dutta, G., Basu, S.;Vaidyanathan, K. (2005). “Term Structure Estimation in Illiquid Government Bond Markets: An Empirical Analysis”. Journal of Emerging Market Finance, Vol 4, pp 63-80.
- Filipovic, D. (2009). “Term Structure Models”. Springer Finance.
- Harvey, A. (1992). “Forecasting, structural time series models and the Kalman filter”. Cambridge University Press.
- Jamieson, D. (2001). “Affine Term-Structure Models: Theory and Implementation”. Working Paper - Bank of Canada.
- Jamieson, D.;Scott, G. (2002). “Exponentials, Polynomials, and Fourier Series: More Yield Curve Modelling at the Bank of Canada”. Working Paper - Bank of Canada.
- Kalman, R. (1960). “A New Approach to Linear Filtering and Prediction Problems”. Journal of Basic Engineering 82, pp 35-45.
- Linke, Y., Mader, M., Mader, W., Schelter, B., Sommerlade, L., Timmer, J. (2014). “A Numerically Efficient Implementation of the Expectation Maximization Algorithm for State Space Models”. Applied Mathematics and Computation, Vol 241, pp 222-232.
- Mara, G. (2017). Temas Generales para las Curvas de BEVSA. https://web.bevsa.com.uy/Descargas/Temas/20Generales/20para/20las/20Curvas.pdf.
- Musiela, M.;Rutkowski M. (2005). “Martingale Methods in Financial Modeling”. Second Edition, Springer.
- Nelson, C.;Siegel, A. (1987). “Parsimonious Modeling of Yield Curves”. Journal of Business, Vol 60, No 4, 473-489.
- Orsag, S.;Zoricic, D. (2013). “Parametric Yield Curve Modeling in an Illiquid and Undeveloped Financial Market”. Journal of Economics. Vol 4, 3.
- Svensson, L. (1994). Estimating and Interpreting Forward Interest Rates: Sweden 1992-1994. Institute for International Economic Studies. Papers 579.
- Vasicek, O. (1977). “An equilibrium characterization of the term structure”. Journal of Financial Economics 5, pp 177-188.
- Xie, C., Chen, H.;Yu, X. (2006). “Yield Curve Estimation in the Illiquid Market: framework, models and empirical study”. International Journal of Information Technology & Decision Making, Vol 5, 3.
Sobre la revista
ISSN 1666-5112 | eISSN 1669-1830
Cuadernos del CIMBAGE es una revista semestral, que incluye trabajos sobre aplicaciones de la lógica y la matemática a temas de gestión y economía.
DIRECTOR GENERAL
Javier I. García Fronti
CODIRECTORES
Alberto H. Landro
María José Bianco
María José Fernández
SECRETARIA DE REDACCIÓN
Raquel Soto