- Instituto de Demografía y Estadística. Facultad de Ciencias Económicas. Universidad Nacional de Córdoba.
- Instituto de Demografía y Estadística. Facultad de Ciencias Económicas. Universidad Nacional de Córdoba.
- Instituto de Demografía y Estadística. Facultad de Ciencias Económicas. Universidad Nacional de Córdoba.
RESUMEN
Palabras clave: Datos de Panel; Rentabilidad Bancaria; Determinantes de la rentabilidad.
ABSTRACT
Keywords: Panel Data; Bank-Profitability; Determinants of profitability.
JEL Code: C23; G21; L2
INTRODUCCIÓN
La economía argentina post devaluación del año 2001, tuvo un período de significativa expansión hasta el año 2011, entrando a partir del 2012 en un estancamiento hasta el 2015. A partir del 2016 hubo cambios regulatorios y contextuales que sin duda han impactado en el sistema bancario argentino. Los estudios de rentabilidad bancaria sobre los cuales este trabajo está basado usan modelos lineales para estimar el impacto en la rentabilidad de distintos factores. En los estudios aplicados al caso argentino, sólo se trabajó con determinantes internos, sin considerar factores sectoriales, tales como la concentración. Por otro lado, en ellos se aplica una metodología estadística que ignora la estructura de panel en un caso (Werbin, 2010) o se utiliza un modelo de efectos aleatorios sin garantizar su validez (Díaz, et al., 2017).
Este es el marco en el que se plantea el presente trabajo, el cual tiene como objetivo estudiar los determinantes de la rentabilidad bancaria utilizando factores internos, como así también un índice de concentración propio del sector. Al mismo tiempo, se analiza cuidadosamente diversas estrategias de modelación para datos de panel, realizando las pruebas pertinentes a fin de escoger la especificación más apropiada. Este proceso de selección culmina en un modelo de efectos fijos, que es el más utilizado en paneles microeconométricos (Cameron y Trivedi, 2010). La estimación está basada en los reportes de los balances disponibles en el Banco Central de la República Argentina, correspondiente a los períodos comprendidos entre el 2005 y el 2018. Los resultados obtenidos muestran, en concordancia con lo esperado, que los factores específicos de los bancos afectan la rentabilidad, como así también el Índice de Herfindahl.
El trabajo se ha estructurado como sigue: en primer lugar, se expone la revisión de la literatura, en la que se analizan la información utilizada para explicar la rentabilidad de los bancos y los modelos empleados para obtener las estimaciones. Esta revisión ha permitido detectar que no hay trabajos empíricos que estudien conjuntamente la dependencia temporal y transversal en datos de panel aplicados al sector bancario. En la tercera sección se expone la metodología utilizada para estimar el modelo y en la siguiente los resultados obtenidos. El trabajo finaliza exponiendo las principales conclusiones.
MODELOS DE RENTABILIDAD BANCARIA: UNA REVISIÓN DE LA LITERATURA
Existen numerosos estudios sobre los determinantes de la rentabilidad bancaria. Entre esos trabajos, se mencionan a continuación los directamente relacionados al modelo propuesto.
Molineux y Thorton (1992) plantean un modelo para cuantificar el impacto de los determinantes de la rentabilidad sobre activos (ROA) y sobre Patrimonio Neto (ROE) para una muestra de bancos europeos, en el período 1986-1989. Trabajan con variables independientes externas e internas. Entre las primeras consideran cinco variables por país y por año: una binaria que clasifica al banco como Público o Privado, el porcentaje de Concentración de los diez bancos con mayor activo, la Tasa de Interés de los bonos de largo plazo, el crecimiento de la Oferta Monetaria y el porcentaje de crecimiento del Índice de Precios. Las variables internas que incluyen son tres ratios en relación al Activo: Capital, DDI (Disponibilidades + Depósitos + Inversiones en Bonos sobre activos) y Gastos Administrativos. En su trabajo resultan variables significativas relacionadas positivamente al ROA, Capital, Concentración bancaria y, si el banco es Público, negativamente significativa resulta la variable DDI. Estiman un modelo lineal para cada año por Mínimos Cuadrados Ordinarios (OLS).
Naceur y Goaied (2001) proponen un modelo para explicar el desempeño de los bancos en Túnez en el período 1980-1985. Toman como variables dependientes ROA y ROE, usando como predictoras la Productividad Laboral, Productividad del Capital, Tamaño, Capitalización, Composición de Cartera, Cotización en Bolsa y Reformas Financieras. Usan un modelo de efectos fijos. En este modelo los determinantes de la rentabilidad que resultan más significativos son la productividad laboral, composición de cartera, productividad del capital y capitalización.
Naceur (2003) introduce mejoras, siguiendo al trabajo Naceur y Goaided (2001), incrementando los períodos considerados 1980-2000, considerando variables adicionales explicativas de la rentabilidad bancaria además de considerar tres modelos de regresión: OLS, un modelo de efectos fijos y otro de efectos aleatorios, por el cual opta finalmente. Considera variables macroeconómicas, inflación y PBI; introduce variables que miden el tamaño relativo de cada banco y del propio sistema a través de dos cocientes, el valor de mercado en relación al patrimonio neto y el valor total de mercado del sistema en relación al PBI. Considera además la influencia de la concentración bancaria a través del Índice de Herfindahl.
Bodla y Verma (2006) analizan los determinantes de la rentabilidad de los bancos públicos en India en el período 1991 hasta 2003. Las variables consideradas son: beneficio neto como proxy de rentabilidad y como variables independientes incluyen Spread, Ingresos no provenientes de intereses, los ratios Créditos/Depósitos y Activos no productivos/Activos. Además, incluyen Previsiones y contingencias, Gastos Operativos, Negocios por empleado, Beneficio por empleado. En este estudio los autores estiman un modelo OLS para cada período.
Athanosoglou, et al., (2008) analizan los factores determinantes de la rentabilidad (ROA y ROE) para los bancos griegos, en el período 1985-2001. Las variables independientes consideradas son externas, propias del sector y macroeconómicas, e internas, determinantes de cada banco. Entre las primeras consideran cuatro variables por año: una binaria Público/Privado, el índice de Concentración de Herfindhal-Hirschman, la Tasa de Inflación del período o las tasas de Interés de los bonos a 10 años y la desviación respecto del ciclo económico. Las variables internas que incluyen son los ratios Patrimonio Neto/Activo, Previsiones/Préstamos, tasa de cambio del Ingreso Bruto/Personal, Gastos Administrativos/Activo, log del Activo y log del cuadrado del Activo. Encuentran que todos los determinantes específicos del banco, con la excepción del tamaño, afectan significativamente la rentabilidad bancaria. Metodológicamente, proponen un modelo de panel dinámico, estimado por efectos fijos (FE) en el paradigma de Arellano & Bond, luego de rechazar un modelo dinámico de efectos aleatorios (RE). Consideran que la estimación está exenta de los posibles inconvenientes de una estimación por variables instrumentales vía GMM por tener un panel con T relativamente grande (T=17).
Werbin (2010) en su tesis doctoral hace un estudio similar al de Bodla y Verma (2006) para bancos argentinos en el período 2005-2007, estimando doce regresiones por OLS, una para cada año y para cada grupo de bancos: Típicos, Comerciales, Personales y Otros.
Díaz, et al., (2017) efectúan un análisis similar al de Werbin, ampliando el período de estudio a los años 2005-2010, aplicando un modelo lineal mixto para la estimación del modelo de rentabilidad en cada uno de los clusters.
Salvo en el trabajo de Athanosoglou, et al., (2008), Naceur y Goaied (2001), Naceur (2003) y en el de Díaz, et al., (2017), en los trabajos arriba mencionados, no se considera la naturaleza longitudinal de los datos ni se tratan cuestiones acerca de la calidad de ajuste de los modelos. Ninguno de estos trabajos hace consideraciones sobre correlación cross-section.
Este trabajo mira los determinantes de la rentabilidad bancaria concentrándose en el estrato de bancos Típicos usando un modelo de panel de efectos fijos. Amplía el panel de Díaz et al (2017) al período 2005-2018 y cambia la respuesta por ROA; adicionalmente se consideran otras variables, similares a las consideradas en Athanosoglou, et al., (2008), y se comparan varias metodologías de estimación. En particular, se consideraron modelos de panel dinámicos, no resultando significativa la variable lagged, indicando esto que los ajustes a los contextos cambiantes son inmediatos, optando por un modelo FE no dinámico. Para este modelo se usaron estimaciones robustas de las varianzas por Driscoll & Kraay (1998) a los fines de evitar asignar carácter significativo erróneamente a las variables independientes. La determinación de pertenencia a los estratos “bancos típicos”, “comerciales”, “personales” y “otros bancos”, se ha tomado del trabajo Vargas, et al., (2018)[1], en donde el tratamiento se realiza por medio de estadística robusta.
METODOLOGÍA
En los datos de panel las observaciones se miden en los mismos períodos de tiempo, por lo que a menudo presentan dependencias transversales y temporales (Feng y Seasholes (2004) y Hirshleifer y Teoch (2003), entre otros). En este panel, la estructura jerárquica incluye dos niveles, año de medición, denotado con el subíndice ![]() y banco, denotado con el subíndice
y banco, denotado con el subíndice ![]() .
.
El modelo pooled OLS es el más restrictivo, ya que especifica que la ordenada y los coeficientes son constantes
![]()
donde ![]() es la rentabilidad del banco
es la rentabilidad del banco ![]() en el año
en el año ![]() ,
, ![]() es la constante,
es la constante, ![]() son las variables predictoras y
son las variables predictoras y ![]() el término de error. La regresión pooled OLS ignora la autocorrelación y, cuando la misma es considerable, subestima los errores standard de los estimadores.
el término de error. La regresión pooled OLS ignora la autocorrelación y, cuando la misma es considerable, subestima los errores standard de los estimadores.
Los Modelos Sujeto Específico incluyen una ordenada ![]() para cada grupo, que capta la heterogeneidad no observada que induce la dependencia temporal
para cada grupo, que capta la heterogeneidad no observada que induce la dependencia temporal
![]()
Las ![]() son variables aleatorias con distribución normal,
son variables aleatorias con distribución normal, ![]() e independiente de
e independiente de ![]() . La suma de ambas varianzas es la varianza total, y la proporción de esta variabilidad debida a la varianza entre grupos se denomina Coeficiente de correlación intraclase.
. La suma de ambas varianzas es la varianza total, y la proporción de esta variabilidad debida a la varianza entre grupos se denomina Coeficiente de correlación intraclase.
![]()
En el modelo de Efectos Fijos, ![]() es una variable aleatoria no observada, potencialmente correlacionada con las regresoras observadas, mientras que en el modelo de Efectos Aleatorios
es una variable aleatoria no observada, potencialmente correlacionada con las regresoras observadas, mientras que en el modelo de Efectos Aleatorios ![]() es una variable aleatoria no observada independiente de regresoras observadas. La estimación del modelo de Efectos Fijos es a través de un Estimador Dentro: se estima un modelo OLS al siguiente modelo de regresión transformado:
es una variable aleatoria no observada independiente de regresoras observadas. La estimación del modelo de Efectos Fijos es a través de un Estimador Dentro: se estima un modelo OLS al siguiente modelo de regresión transformado:
![]()
donde ![]() son las medias de grupos, y
son las medias de grupos, y ![]() son las medias de todas las observaciones.
son las medias de todas las observaciones.
En el modelo de RE se pueden calcular los valores predichos ![]() ; mientras que en el modelo de FE
; mientras que en el modelo de FE![]() no es estimable consistentemente para paneles cortos. El modelo FE permite identificar sólo el efecto marginal para regresoras que varían en el tiempo. Si el verdadero modelo es FE, tanto pooled OLS como RE arrojan estimadores inconsistentes. Si el modelo de Efectos Aleatorios es correcto, pooled OLS subestima varianzas y son necesarios estimadores robustos a heterocedasticidad y autocorrelación.
no es estimable consistentemente para paneles cortos. El modelo FE permite identificar sólo el efecto marginal para regresoras que varían en el tiempo. Si el verdadero modelo es FE, tanto pooled OLS como RE arrojan estimadores inconsistentes. Si el modelo de Efectos Aleatorios es correcto, pooled OLS subestima varianzas y son necesarios estimadores robustos a heterocedasticidad y autocorrelación.
Para el modelo pooled OLS, FE y RE, los estimadores robustos están basados en la corrección de White (1980), conocidos como estimadores sándwich y permiten obtener estimadores de los errores estándar consistentes en presencia de heterocedasticidad y autocorrelación, siempre que se cumpla la independencia transversal (Baltagi, 2008).
Por otro lado, numerosos estudios indican que los paneles microeconométricos exhiben dependencia cross-section. La prueba de Pesaran (Pesaran, 2004) es aplicable a modelos de panel que se basa en el promedio de coeficientes de correlación de parejas de los residuos OLS de las regresiones individuales en el panel. Más precisamente, si el modelo es
![]()
y
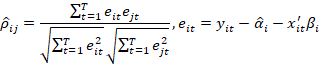
el estadístico para la prueba de Pesaran es
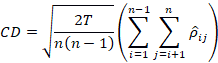
Bajo ![]() ,
, ![]() y
y ![]() tienen distribución
tienen distribución ![]() .
.
Para incorporar la dependencia cross-section, Driscoll y Kraay (1998) proponen un estimador no paramétrico de la matriz de covarianza consistente y “robusto” a varias formas de dependencia transversal y temporal. Ese estimador es implementado en Stata a través del programa xtscc (D. Hoechle, Stata Journal 2007, v.7, n.3.) para pooled OLS y regresión de efectos fijos. Driscoll-Kraay calcula los errores estándares como la raíz de la diagonal de la matriz de covarianzas asintótica
![]()
donde ![]() es (Newey West, 1987)
es (Newey West, 1987)
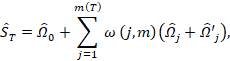
![]() es el lag hasta donde los errores pueden estar correlacionados,
es el lag hasta donde los errores pueden estar correlacionados,
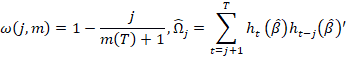
y ![]() captura la correlación promedio del panel
captura la correlación promedio del panel ![]()
Tabla 1: Variables respuesta y covariables
|
Variable |
Concepto |
Etiqueta |
Efecto Esperado |
|
Variable respuesta |
|
|
|
|
Rentabilidad |
Beneficio/Activo |
ROA |
|
|
Determinantes |
|
|
|
|
Capital |
Patrimonio Neto/Activo |
Capital |
Positivo |
|
Riesgo Crediticio |
Previsiones/Préstamos |
Riesgo |
Negativo |
|
Productividad |
Ingresos Brutos/DotPersonal |
ProdPersonal |
Positivo |
|
Gestión de Gastos |
Gastos Administrativos/Activo |
Gestión |
Negativo |
|
Tamaño |
log(Activo) |
logActivo |
? |
|
Específicas del sector |
|
|
|
|
Concentración |
Índice de Herfindahl-Hirschman |
hh |
? |
La variable respuesta está representada por el ratio Beneficios/Activos (ROA), que mide la capacidad de un banco para generar beneficios de los activos. Las covariables utilizadas son similares a las utilizadas en Athanasoglou, et al., (2008), las que pueden ser clasificadas en determinantes internos y variables referidas a las características del sector. No se han incluido las variables que representan características macroeconómicas.
El indicador sectorial utilizado, derivado del Índice de Herfindahl-Hirschman se calculó como el cuadrado de la proporción del activo del banco respecto de la sumatoria de activos del sistema.
ESTIMACIÓN
El grupo objeto de análisis está constituido por 25 bancos típicos, analizados durante 14 años, en el período comprendido entre 2005 y 2018, ambos incluidos. Para cada uno de ellos se tomaron los estados financieros de los últimos catorce años, conformando un panel desbalanceado configurado por 319 observaciones de 24 bancos[2]. Se excluyeron del panel siete observaciones con ROA negativo y otras diez influyentes en el modelo pooled OLS. La estructura de los datos, correspondiente a variables que se miden para cada banco en distintos años, conduce a la necesidad de trabajar con modelos para datos correlacionados. Se puede modelar la dependencia dentro de los bancos dividiendo el término residual en dos partes: una componente específica![]() de cada banco
de cada banco ![]() y constante entre años y otra componente
y constante entre años y otra componente ![]() que capta la variabilidad dentro del grupo. Esto permite descomponer la variabilidad entre unidades y dentro de las mismas y la componente específica permite captar la heterogeneidad individual no observable.
que capta la variabilidad dentro del grupo. Esto permite descomponer la variabilidad entre unidades y dentro de las mismas y la componente específica permite captar la heterogeneidad individual no observable.
La metodología de análisis se aborda de la siguiente forma: en primer lugar, se prueba si hay efectos individuales y luego si hay diferencia entre los estimadores obtenidos a través de Efectos Fijos (FE) o Efectos Aleatorios (RE). Finalmente, se usa la prueba de Pesaran para examinar la dependencia espacial. Para verificar si hay efectos específicos, se prueba si la variabilidad de la ordenada específica ![]() es significativa, utilizando para ello una prueba
es significativa, utilizando para ello una prueba ![]() que testea si
que testea si ![]() . Con un nivel del
. Con un nivel del ![]() se rechaza esa hipótesis[3], por lo que se continúa con la estimación de modelos con ordenadas específicas (modelo 2). Los métodos de estimación más utilizados para estos modelos son los de FE y RE. En el primero la ordenada específica
se rechaza esa hipótesis[3], por lo que se continúa con la estimación de modelos con ordenadas específicas (modelo 2). Los métodos de estimación más utilizados para estos modelos son los de FE y RE. En el primero la ordenada específica ![]() es una variable aleatoria no observada, potencialmente correlacionada con las regresoras observadas. En cambio, en el RE se supone que es una variable aleatoria no observada independiente de las regresoras. En este trabajo el cumplimiento de este supuesto es verificado por el test de Hausman, que prueba la hipótesis de no diferencias entre los estimadores FE y RE, la que es rechazada a un
es una variable aleatoria no observada, potencialmente correlacionada con las regresoras observadas. En cambio, en el RE se supone que es una variable aleatoria no observada independiente de las regresoras. En este trabajo el cumplimiento de este supuesto es verificado por el test de Hausman, que prueba la hipótesis de no diferencias entre los estimadores FE y RE, la que es rechazada a un ![]() , concluyendo que es aconsejable la estimación de un modelo FE[4]. Como numerosos estudios indican que los paneles microeconométricos exhiben dependencia cross-section, también se examinó si en este panel se observa esa relación. Para ello se aplicó la prueba de Pesaran[5], que se basa en el promedio de coeficientes de correlación de parejas de los residuos OLS de las regresiones individuales en el panel. La evidencia de la prueba permite concluir que sí hay dependencia espacial[6]. Por ello, también se estima el modelo utilizando la corrección en FE de Driscoll y Kraay (1998), que incorpora esa dependencia usando un estimador no paramétrico para la matriz de covarianza consistente y robusto a varias formas de dependencia transversal y temporal[7].
, concluyendo que es aconsejable la estimación de un modelo FE[4]. Como numerosos estudios indican que los paneles microeconométricos exhiben dependencia cross-section, también se examinó si en este panel se observa esa relación. Para ello se aplicó la prueba de Pesaran[5], que se basa en el promedio de coeficientes de correlación de parejas de los residuos OLS de las regresiones individuales en el panel. La evidencia de la prueba permite concluir que sí hay dependencia espacial[6]. Por ello, también se estima el modelo utilizando la corrección en FE de Driscoll y Kraay (1998), que incorpora esa dependencia usando un estimador no paramétrico para la matriz de covarianza consistente y robusto a varias formas de dependencia transversal y temporal[7].
RESULTADOS EMPÍRICOS
Por lo expuesto, se considera que el mejor modelo que ajusta a este panel es el modelo de efectos fijos con la corrección de Driscoll y Kraay. Salvo por Productividad, las varianzas con la corrección de White (estimación robusta) son mayores a las estimadas por Driscoll y Kraay. En el caso de la variable Riesgo Crediticio, la estimación por Driscoll y Kraay la tornan significativa. (ver la tabla 2 de estimaciones por los distintos métodos más abajo). Por otro lado, el algoritmo de efectos fijos no sólo asegura estimaciones consistentes para los parámetros, sino también produce residuos que tienen una distribución aproximadamente normal, como se aprecia en la siguiente figura.
Figura 1: Distribución de los residuos del modelo de efectos fijos con corrección de Driscoll y Kraay
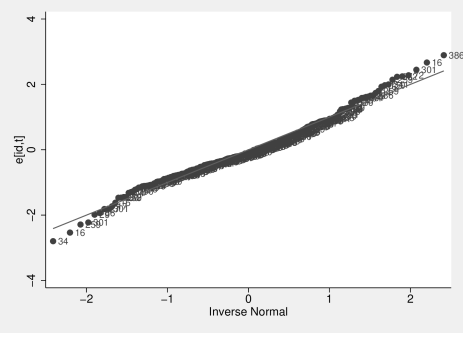
El banco Patagonia, rótulo 34, en el año 2007, el banco Citibank, rótulo 16, en el año 2005 y el Nuevo Banco de Entre Ríos, rótulo 386, en el año 2006 presentan los valores más bajos y más alto entre los residuos estandarizados. El coeficiente de correlación intraclásica (![]() ) indica que una parte significativa de la variabilidad total se debe a la variabilidad entre los bancos, siendo esta heterogeneidad la que se prueba con el test
) indica que una parte significativa de la variabilidad total se debe a la variabilidad entre los bancos, siendo esta heterogeneidad la que se prueba con el test ![]() (ver nota al pie Nro. 3).
(ver nota al pie Nro. 3).
Tabla 2: Estimaciones por diferentes métodos.
|
Variable |
PoolRob |
re |
fe |
feRob |
feDris |
|
capital |
29.3178 |
24.5893 |
21.9725 |
21.9725 |
21.9725 |
|
|
2.1200 |
2.0588 |
2.4431 |
3.6378 |
2.4619 |
|
|
13.8291 |
11.9434 |
8.9935 |
6.0400 |
8.9251 |
|
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
|
riesgo |
-14.7948 |
-11.9263 |
-9.5605 |
-9.5605 |
-9.5605 |
|
|
4.3045 |
3.8799 |
4.0790 |
6.6474 |
2.5575 |
|
|
-3.4371 |
-3.0739 |
-2.3438 |
-1.4382 |
-3.7382 |
|
|
0.0007 |
0.0021 |
0.0198 |
0.1638 |
0.0025 |
|
ProdPersonal |
0.2000 |
0.1859 |
0.1713 |
0.1713 |
0.1713 |
|
|
0.0389 |
0.0269 |
0.0352 |
0.0688 |
0.0421 |
|
|
5.1479 |
6.8987 |
4.8685 |
2.4914 |
4.0689 |
|
|
0.0000 |
0.0000 |
0.0000 |
0.0204 |
0.0013 |
|
gestión |
2.0893 |
1.1419 |
-0.1939 |
-0.1939 |
-0.1939 |
|
|
2.5164 |
2.9000 |
3.5063 |
5.2214 |
2.9707 |
|
|
0.8302 |
0.3938 |
-0.0553 |
-0.0371 |
-0.0653 |
|
|
0.4070 |
0.6937 |
0.9559 |
0.9707 |
0.9489 |
|
logActivo |
0.0730 |
0.1155 |
0.1699 |
0.1699 |
0.1699 |
|
|
0.0522 |
0.0638 |
0.1074 |
0.1719 |
0.1803 |
|
|
1.3982 |
1.8102 |
1.5821 |
0.9885 |
0.9427 |
|
|
0.1630 |
0.0703 |
0.1147 |
0.3332 |
0.3630 |
|
hh |
0.0031 |
0.0032 |
0.0032 |
0.0032 |
0.0032 |
|
|
0.0006 |
0.0006 |
0.0006 |
0.0006 |
0.0006 |
|
|
5.3087 |
5.5347 |
5.3396 |
5.1784 |
5.6650 |
|
|
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0001 |
|
cons |
-4.1603 |
-4.0989 |
-4.2515 |
-4.2515 |
-4.2515 |
|
|
0.7342 |
0.7993 |
1.0156 |
1.3358 |
1.4398 |
|
|
-5.6668 |
-5.1281 |
-4.1861 |
-3.1827 |
-2.9528 |
|
|
0.0000 |
0.0000 |
0.0000 |
0.0041 |
0.0112 |
|
|
|
|
0.4963 |
0.6518 |
0.6518 |
|
|
|
|
0.9252 |
0.9252 |
0.9252 |
|
|
|
|
0.2235 |
0.3317 |
0.3317 |
|
legend: |
b/se/t/p |
|
|
|
|
Los coeficientes y p-valores expuestos en la Tabla 2 revelan que, entre los determinantes de los bancos, las variables Capital, Productividad del Personal y Tamaño, son estadísticamente significativas y con efectos positivas mientras que Riesgo Crediticio tiene un impacto significativo negativo. Estos resultados están en línea con la teoría que sostiene que el tamaño y la productividad inciden positivamente, en tanto que la mayor exposición al riesgo de crédito se asocia normalmente con la disminución de la rentabilidad de los bancos. En cuanto a la variable externa Índice de Herfindahl, ésta tiene un efecto positivo en la rentabilidad de los bancos.
CONCLUSIONES
En este trabajo se estudian los factores que impactan en la rentabilidad bancaria utilizando factores internos, como así también un índice de concentración propio del sector. Cabe señalar que el uso de este índice, que tiene un impacto positivo en la rentabilidad, resulta novedoso para este tipo de trabajo.
Se analizaron diversas estrategias de modelación para datos de panel. En primer lugar, la variabilidad del efecto específico, invariante en el tiempo, conduce a rechazar la hipótesis de la pertinencia de un modelo pooled OLS. Usando la prueba de Hausman, se concluye en favor de un modelo de efectos fijos. Finalmente, la prueba de Pesaran rechaza la hipótesis de independencia transversal, aconsejando una estimación de varianzas que incorpore esta correlación. Esto constituye una de las contribuciones de este trabajo que lo distingue de los estudios previos sobre rentabilidad bancaria. Este análisis conduce a la estrategia óptima, esto es, un modelo de efectos fijos con la corrección de Driscoll y Kraay para las varianzas.
Entre las variables que impactan positivamente en la rentabilidad de los bancos típicos se encuentran las variables Capital, Productividad del Personal, Tamaño e Índice de Concentración en tanto que Riesgo Crediticio tiene un impacto significativo negativo.
[1]Robust Clustering of Banks in Argentina, Vargas, J.M., Díaz, M. y García, F., Enviado para su publicación.
[2]En la estimación del modelo se excluyó el Banco de San Juan S.A. por presentar varios años con resultados atípicos. Se incluyeron entre 13 y 14 balances en 22 de los 24 bancos analizados, publicados por el Banco Central de la República Argentina, para los meses de diciembre de los años 2005 al 2018
[3]El valor observado de la prueba F es ![]() con un p-value=0.00.
con un p-value=0.00.
[4]El valor observado de la prueba ![]() es
es ![]() con un p-value= 0.086.
con un p-value= 0.086.
[5]Pesaran M.H. (2004).
[6]El valor observado del test de Pesaran es , ![]() con un p-value=0.0009.
con un p-value=0.0009.
[7]Implementado en STATA a través del programa xtscc (D.Hoechle, Sta Journal 2007, v.7, n.3) para pooled OLS y FE.
Referencias
- Athanasoglou, P. P., Brissimis, S. N., Delis, M. D. (2008). Bank-specific, industry-specific and macroeconomic determinants of bank profitability. Journal of international financial Markets, Institutions and Money, 18(2), 121-136.
- Baltagi, Badi H. (2013). Econometric Analysis of Panel Data. Wiley.
- Naceur, S. B., Goaied, M. (2001). The determinants of the Tunisian deposit banks' performance. Applied Financial Economics, 11(3), 317-319.
- Naceur, S. B. (2003). The determinants of the Tunisian banking industry profitability: Panel evidence. Universite Libre de Tunis working papers, 11(3), 317-319.
- Bodla, B. S., Verma, R. (2006). Determinants of profitability of banks in India: A multivariate analysis. Journal of Services Research, 6(2), 75-89.
- Cameron, A. Colin, Pravin K. Trivedi (2009). Microeconometrics Using Stata. Stata Press.
- Díaz, Margarita, Eliana Werbin, Fernando García. (2017). Determinantes de Rentabilidad: Una Aplicación a Bancos en Argentina en el Período 2005-2010. Revista Internacional LEGIS de Contabilidad y Aditoría, no. 71 (July): 95–114.
- Driscoll, J. C., Kraay, A. C. (1998). Consistent covariance matrix estimation with spatially dependent panel data. Review of economics and statistics, 80(4), 549-560.
- Feng, L., Seasholes, M. S. (2004). Correlated trading and location. The Journal of Finance, 59(5), 2117-2144.
- Hirshleifer, D., Hong Teoh, S. (2003). Herd behaviour and cascading in capital markets: A review and synthesis. European Financial Management, 9(1), 25-66.
- Hoechle, D. (2007). Robust standard errors for panel regressions with cross-sectional dependence. The Stata journal, 7(3), 281-312.
- Pesaran, M. H. (2004). “General Diagnostic Tests for Cross Section Dependence in Panels”. Cambridge Working Papers in Economics 0435, Faculty of Economics, University of Cambridge.
- Vargas, J.M., M. Díaz, F. García. (2018) Robust Clustering of Banks in Argentina.
- Werbin, Eliana. (2010). “Los Determinantes de La Rentabilidad de Los Bancos En Argentina (2005 – 2007)”. PhD thesis, Universidad Nacional de Córdoba; Facultad de Ciencias Económicas.
Sobre la revista
ISSN 1666-5112 | eISSN 1669-1830
Cuadernos del CIMBAGE es una revista semestral, que incluye trabajos sobre aplicaciones de la lógica y la matemática a temas de gestión y economía.
DIRECTOR GENERAL
Javier I. García Fronti
CODIRECTORES
Alberto H. Landro
María José Bianco
María José Fernández
SECRETARIA DE REDACCIÓN
Raquel Soto