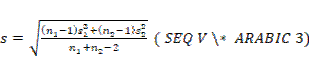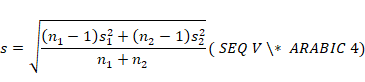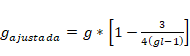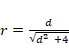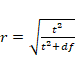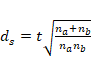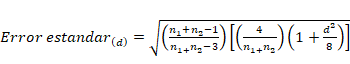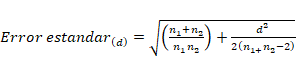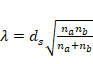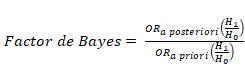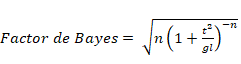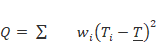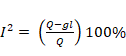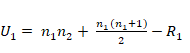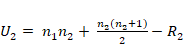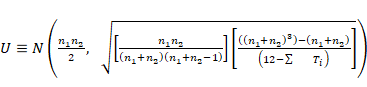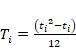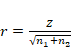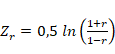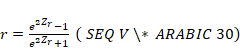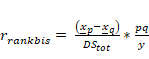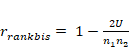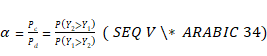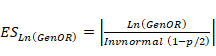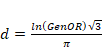La prueba de hipótesis ha reinado con tranquilidad en el ámbito científico durante el siglo pasado. Esto ha cambiado sustancialmente, en especial durante este último decenio. Se han desarrollado técnicas, ahora más fácilmente aplicables debido al avance tecnológico, que conducen a los investigadores a hacerse preguntas sobre su quehacer cotidiano.

Estas preguntas son incómodas. Cuestionan la tranquilidad de las afirmaciones realizadas. Me dio significativo. Bueno, podemos publicar los resultados. ¿Cómo? ¡Ah! ¡Tenemos que hacer los intervalos de confianza! ¿Cuántas más chances tiene nuestra hipótesis alternativa de ser cierta en relación a la hipótesis nula? ¿En qué medida afecta la variable predictora, factor o independiente a nuestra variable resultado o dependiente de acuerdo con nuestro estudio? Especialmente cuando no nos dio significativa nuestra prueba de hipótesis, ¿qué potencia tenía nuestro estudio? Si encontramos resultados divergentes, ¿qué hay que hacer?

Este trabajo intenta divulgar una serie de problemas y soluciones ofrecidas por los investigadores a la cuestión de la prueba de hipótesis en el caso particular de la diferencia de medias en muestras independientes.

Una vez que obtenemos un resultado particular en nuestra prueba de hipótesis surgen una serie de interrogantes que han sido respondidos con los siguientes abordajes.

Si la prueba no resultó estadísticamente significativa, ¿qué potencia tenía nuestra prueba, qué probabilidad tenía de que exista una verdadera diferencia y nosotros por nuestro abordaje no pudimos captarla? Y si resultó significativa, es decir, si consideramos la existencia de un efecto. ¿Qué dimensión tiene ese efecto? En cualquier caso ¿Qué probabilidad tienen estas hipótesis de ser ciertas?

Durante los últimos años se ha observado una creciente producción en todos estos temas, lo que fue acompañado también, por un gran desarrollo de recursos informáticos que podrán ayudar al investigador en su actividad cotidiana.

Quien se haya interiorizado en estos temas podrá apreciar que existe a la fecha una creciente resistencia a la utilización de la prueba de hipótesis por parte de los teóricos en la materia, pero que sin embargo sigue siendo utilizada por los investigadores, muchas veces sin la adecuada conciencia de los problemas que conlleva.

En resumen, la prueba de hipótesis nos informa acerca de cuan im/probables son los resultados obtenidos en nuestra muestra a la luz de la hipótesis nula.

Siendo esquemáticos, si el test resulta significativo, estamos justificados para afirmar la hipótesis alternativa, pero no tenemos idea de la dimensión del efecto entre las variables. Aquí es donde se plantea la necesidad de medir el tamaño del efecto, y sus respectivos intervalos de confianza. Si mantenemos esa diferencia tal como se nos ofrece por ejemplo en una prueba t de Student podremos obtener una diferencia y un intervalo de confianza para dicha relación. Sin embargo, muchas veces estamos interesados en una diferencia estandarizada. Tendremos así una medida del tamaño del efecto medida en unidades de desviación combinada (‘pooled’).

Es decir, a la evidencia sobre la existencia de un determinado efecto, le sumaremos entonces una información en relación al tamaño de ese efecto.

Cuando diseñemos nuestra investigación deberíamos tener en cuenta la capacidad de nuestro abordaje para conocer qué probabilidad tendremos de obtener un resultado no significativo cuando la hipótesis nula sea falsa, es decir lo que se conoce como potencia de la prueba (P(1-error tipo II)). E incluso ante la eventualidad de obtener una p no significativa tendríamos que evaluar la posibilidad de que nos encontremos ante un error de tipo II. Es decir, que exista un efecto, que además tenga evidentemente algún tamaño, pero que no podremos eventualmente afirmarlo debido al deficiente poder de la prueba que hemos aplicado. Esto es realmente importante cuando por las razones que sean se ha operado con un dispositivo de prueba de hipótesis deficiente en términos de la cantidad de casos disponibles en el estudio.

Finalmente, para un estudio particular, tanto en el caso de obtener significación estadística como en el caso contrario, podremos responder a la pregunta sobre la probabilidad de que la hipótesis alternativa (ídem para la nula) sea cierta según nuestros datos (y eventualmente otros estudios).

En particular, esto será importante cuando exista evidencia contradictoria entre diversos estudios, tanto a nivel de significación (efecto) como a nivel de los tamaños de efecto obtenidos y se sugiera realizar un estudio capaz de generar un resultado que unifique los diversos estudios.

El tamaño del efecto viene a dar una respuesta complementaria a una serie de problemas derivados de la utilización del test de hipótesis (en inglés, Null hypotesis statistical testing (NHST), en castellano denominado con varios términos: contraste de hipótesis, test de hipótesis, prueba de significación, etc.).

El test de hipótesis (NHST) es el método dominante para probar teorías utilizando estadísticas. Según Field, es irresistible porque ofrece un camino, un marco para decidir si creer en una hipótesis particular. También es atractivo enseñarlo porque incluso si los estudiantes no entienden la lógica detrás de la prueba, la mayoría puede llegar a comprender la idea de que un p <.05 es "significativo" y un p> .05 no lo es (2013).

Nos da una receta de cocina de cómo proceder. El modo “correcto” de proceder para mantenerse dentro del ámbito científico y conseguir entonces conclusiones también “correctas”.

Sin embargo, aparecen en este punto toda una serie de críticas a este método que desarrollaremos brevemente en este trabajo.

Estas críticas concluyen en un punto que tomado seriamente invalida los procedimientos que se ajusten exclusivamente a esta lógica. Esta problemática se torna especialmente delicada en momentos en que se ha producido –en particular durante este último decenio- una crisis de reproducibilidad o replicabilidad, es decir, sobre uno de los pilares de la ciencia, tanto en ciencias sociales, biológicas, médicas y psicológicas (Ioannidis, 2014).

¿Qué es la prueba o test de hipótesis?

Se trata de un procedimiento para juzgar si una propiedad que se supone en una población estadística es compatible con lo observado en una muestra de dicha población. Fue iniciada por Ronald Fisher a partir de la consideración de qué probabilidad tiene una hipótesis de que sea rechazada. Posteriormente esta idea fue desarrollada por Jerzy Neyman y Karl Pearson en los términos más conocidos actualmente como confrontación de hipótesis nula y alternativa.

El planteamiento básico de Fisher fue que es necesario calcular la probabilidad de un evento y evaluar esta probabilidad dentro del contexto de la investigación. Para Fisher un p = 0,01 nos estaría ofreciendo una fuerte evidencia para respaldar una hipótesis, y tal vez un p = 0,20 sería una evidencia débil, aunque nunca dijo que p = 0,05 era, de alguna manera, un número especial.

En contraste con Fisher, Neyman y Pearson creían que las declaraciones científicas deberían ser comprobables, para ello sería necesario declarar una hipótesis o predicción teórica a partir de la evidencia ofrecida por la experiencia.

Esta hipótesis se denomina alternativa y se denota por H1 (a veces es también llamada experimental, pero como este término se relaciona con un tipo específico de diseño de investigación, es mejor usar generalmente ‘alternativa’). La hipótesis contrapuesta es llamada nula y se la suele denotar por H0.

Mediante este abordaje, se aborda el problema estadístico considerando una hipótesis determinada, y se intenta dirimir cuál de las dos es la verdadera, tras aplicar el problema a un cierto número de experimentos.

Está fuertemente asociada al concepto estadístico de potencia y a los conceptos de errores de tipo I y II, que definen respectivamente, la posibilidad de tomar un suceso falso como verdadero, o uno verdadero como falso.

Por ejemplo, nosotros podríamos querer determinar si, en una determinada población, dos grupos son distintos en una determinada propiedad o variable, medida, por ejemplo, a través de los respectivos promedios. Lo que se desea saber es si la diferencia hallada en una muestra de los dos grupos fue debida a una cuestión puramente de azar, o se trata de una diferencia que efectivamente se encuentra entre esos grupos en la población. 

En este sentido, la significación estadística es la verosimilitud de que la diferencia entre los dos grupos pueda deberse simplemente a un accidente del muestreo, un error (de tipo I en este caso). Dicho con otras palabras, mide la probabilidad de que la diferencia observada sea del mismo tamaño que la que se hubiera obtenido por azar, incluso en el caso de que no hubiera diferencias entre los dos grupos.

Un resumen de lo señalado puede ser sintetizado en la siguiente tabla:

 

 

Tabla 1. Los errores en el contraste de hipótesis

 

Críticas al test de hipótesis

Existen problemas con el uso de las pruebas de significación, ya que el valor p es resultado de dos cuestiones: del tamaño de las diferencias y del tamaño de la muestra. Se podrían obtener resultados significativos tanto si las diferencias entre los grupos son muy grandes, aunque la muestra fuera pequeña, como si la muestra fuera muy grande, aunque el tamaño de la diferencia fuera pequeño.

Según Meelh (1978 en Morales Vallejo, 2012), autor junto con Cronbach de la concepción más relevante sobre validación de constructo, afirma que “construir la ciencia rechazando hipótesis nulas es un terrible error, un procedimiento básicamente inadecuado, una pobre estrategia científica y una de las peores cosas que han sucedido en la historia de la psicología”.

Nunnally (1960) critica fuertemente el abordaje señalando que "el modelo de comprobación de hipótesis peor utilizado es el de la hipótesis nula, el énfasis en la misma es poco informativo, y en la vida real casi nunca es verdadera".

Jacob Cohen afirma que existe una mala aplicación del razonamiento silogístico en relación al test de hipótesis, por la cual, si se rechaza H0, habría como mínimo una baja probabilidad de tal hipótesis. En este sentido, no es lo mismo, para el autor, que la prueba de hipótesis dé cuenta de que "H0 es verdadera, dados unos datos”, que la correcta interpretación, por la cual, se afirma la probabilidad de obtener unos datos (o aún más extremos) dado que H0 es verdadera (1994).

Muchos otros autores expresan que la práctica de confiar en la significación estadística como si fuera un índice de certeza es peligrosa, un resultado estadísticamente significativo sólo indica que es poco probable que la relación encontrada entre las variables sea debida al azar y, por tanto, esa relación puede ser aceptada como real o meramente existente. No obstante, la significación estadística no proporciona información sobre la fuerza de la relación (tamaño del efecto) o si la relación es reveladora (significación práctica o clínica) (Iraurgi, 2009); Ellis, 2010); Morales Vallejo, 2012).

Esencialmente lo que se afirma es que el test o contraste de hipótesis presenta una serie de fallas para dar cuenta del avance de la ciencia. En primer lugar, trata de dar cuenta de la presencia o ausencia de una relación entre dos o más variables en términos dicotómicos en vez de tratar de dar cuenta de una determinada magnitud entre ellas.

Evidentemente a menos que haya una paridad total entre las variables involucradas, si aumentamos el n, en un determinado momento hallaremos significación estadística. Es decir, perdemos la brújula si procedemos solamente en este sentido. Lo importante justamente será dar cuenta de la magnitud, del cuánto de ese efecto o relación entre variables. Cuando el n es grande incluso pequeñas diferencias pueden resultar significativas. En estos casos será necesario analizar el tamaño de la diferencia en términos prácticos o clínicos, y a falta de esta información particular ceñirse a la estandarización ofrecida por la teoría.

Lamentablemente se suele confundir significación estadística con otro sentido de la palabra “significación”: grande, elocuente, reveladora, importante, valiosa, relevante, representativa. Sentidos muy alejados realmente de la importancia práctica o clínica. Pero esta confusión es muy común (Grissom & Kim, 2012).

Desde la corriente denominada “Nuevas Estadísticas” se señala la importancia de incluir en los trabajos los tamaños de efectos, intervalos de confianza y meta-análisis. Las técnicas no son nuevas, pero adoptarlas ampliamente es algo nuevo para muchos investigadores, así como altamente beneficioso. Una adecuada estrategia de estadísticas requiere desde esta perspectiva la formulación de preguntas de investigación en términos de estimación, en las que las pruebas de hipótesis no tienen necesariamente lugar, basándose en la construcción de estudios acumulados. Esta perspectiva sostiene que la principal dependencia del test de hipótesis es el imperativo de lograr significación estadística, que es la clave para la publicación, el avance profesional, la financiación de la investigación y -especialmente por ejemplo para las compañías farmacéuticas-: las ganancias. Este imperativo explica la publicación selectiva, motiva la selección de datos y el ajuste hasta que el valor p sea suficientemente pequeño. Este procedimiento es engañoso ya que la significación estadística se plantea como verdadera y no requiere reproducibilidad (Cumming, 2014).

También Ioannidis, desde otra perspectiva, cuestiona el modo en que se está llevando adelante el proceso de investigación. En particular afirma que en el ámbito de la salud el 85% de los estudios no son de utilidad (2005). Esta es una afirmación muy fuerte. En este sentido el autor indica que para mejorar la credibilidad y eficiencia en la investigación científica se deben mejorar toda una serie de aspectos que incluyen la investigación colaborativa compartiendo registros e incentivando de reproducción (replicación) de los estudios. También señala umbrales más estrictos para reclamar descubrimientos (p menor a 0,05) y estadísticos más apropiados, en particular enfocando los resultados hacia la estandarización y el meta análisis (2014).

Finalmente, una mirada desde la ciencia económica ilustra también esta preocupación. Ziliak y McCloskey piensan que mayormente sus colegas han centrado su atención en la existencia de relaciones, es decir, sobre las pruebas de significación, opacando la crucial preocupación por la pregunta sobre el tamaño de efecto. Afirman que frecuentemente se ha confundido la significación estadística con la significación económica. El descuido respecto de los tamaños de efecto y la confusión entre significación estadística y significado sustantivo han ofrecido resultados desafortunados: a saber, en ocasiones se ha centrado la preocupación en resultados estadísticamente significativos relativos a pequeños efectos sin su concomitante importancia práctica o teórica, y por el contrario, se han rechazado hipótesis de envergadura dado que no han cumplido con el requisito de superar el umbral requerido de 0,05. (Ziliak & McCloskey, 2008).

El tamaño del efecto

El tamaño del efecto (effect size) es un concepto elaborado por Jacob Cohen en su ya clásico texto sobre el análisis del poder estadístico. Generalmente es utilizado en la investigación biomédica y del comportamiento para referirse a la magnitud de una medida de resultado o a la fuerza de una relación entre dos variables, por lo general una independiente y la otra dependiente (Cohen, 1988; Coe, 2002; Carson, 2004 en Iraurgi, 2009).

El tamaño del efecto se refiere a la magnitud del resultado de lo que efectivamente ocurre, o aquello que se encontraría en el caso de estudiar a la población.

Los efectos que podemos hallar en la configuración de un determinado estudio o experimento nos permiten eventualmente estimar los verdaderos efectos, proceso esencial para la evaluación e interpretación de los resultados. Es según Grissom y Kim el grado en que la hipótesis nula es errónea (2012).

Una de las ventajas más importantes de los índices del tamaño del efecto es que son transformaciones a una escala común, a una escala carente de unidades (correlaciones, diferencias estandarizadas, estimaciones de riesgos, etc.), de modo que los resultados de diferentes estudios pueden ser directamente comparables. Esta característica es la que les hace imprescindibles al realizar estudios meta–analíticos, muy útiles a la hora de resumir, estructurar y acumular el conocimiento científico obtenido en investigaciones empíricas.

Cuando realizamos una prueba de hipótesis una posibilidad es que no encontremos diferencias estadísticamente significativas para un determinado nivel de significación (al aceptar H0). En ese caso pueden pasar dos cosas, que efectivamente no existan diferencias, o que éstas existan, pero no sean captadas por el estudio dado el poder de la prueba. El poder de una prueba estadística depende de tres parámetros: el criterio de significación estadística (error asumido o error de tipo I), la confiabilidad de los resultados de la muestra (el error estándar del estadístico y el tamaño de la muestra) y el "tamaño del efecto" es decir, el grado en que existe el fenómeno (Cohen, 1988).

La fórmula que relaciona estos aspectos podemos encontrarla en Pértegas Díaz y Pita Fernández (2003):

  ,

 

donde representa el valor z de la distribución normal estándar para la potencia de la prueba, n el tamaño de la muestra, d el tamaño del efecto, S el desvío estándar conjunto (que será explicado más adelante) y   representa el valor z de la significación estadística. En el caso de pruebas de doble cola este valor de alfa se divide por 2.

Es decir, el criterio de significación estadística (error de tipo I), la potencia de la prueba (1-error de tipo II), el error estándar del estadístico, el tamaño de la muestra y el tamaño del efecto se hayan fuertemente relacionados.

Los tamaños del efecto agrupados en tres familias

Definimos junto a Grissom que el tamaño del efecto es el grado en que la H₀ es errónea. Sin embargo, esta medición puede ser realizada de diversos modos según el tipo de estudio comprendido:  a) la familia de los coeficientes basados en diferencias (d de Cohen, g de Hedges, delta de Glass y la Diferencia de Riesgos; b) la familia de las correlaciones; y c) la familia de las razones (el riesgo relativo y la odds ratio) (Iraurgi, 2009).

La familia de los tamaños de efecto basados en diferencias

Son estadísticos que estiman la magnitud de la diferencia entre medias aritméticas de los efectos obtenidos bajo un tratamiento en comparación con otro grupo (muchas veces denominado de control). Para obtener medias aritméticas las variables resultado deben ser medidas en un nivel de medición cuantitativo (de intervalos o de razón). En este grupo encontramos la conocida d de Cohen, la Δ (delta) de Glass y la g de Hedges.

Mediante esta familia de coeficientes se pretende valorar el grado de generalidad poblacional de un efecto a partir de la diferencia que se observa entre dos medias, bien de un mismo grupo en dos momentos temporales (lo que se conoce como comparación intra–sujetos), bien de dos grupos diferentes en un mismo momento temporal (comparación inter–sujetos), o bien de dos grupos diferentes en dos momentos temporales diferentes (comparación mixta o inter–intra–sujetos). En estos casos la variable predictora o factor (a veces independiente) está medida en una escala nominal.

El cálculo del tamaño del efecto consiste en hallar la diferencia de medias de ambos grupos y dividir este resultado por una medida de variabilidad, una desviación estándar. Los diferentes estimadores de esta familia del tamaño del efecto se diferencian, precisamente, en qué formula de la variabilidad utilicen, pero todas ellas coinciden en ser una diferencia de medias estandarizada.

Por tanto, se trata de una diferencia de medias estandarizadas que varía de -infinito a +infinito, siendo el valor 0 indicativo de ausencia de efecto (la media de ambos grupos es la misma), de modo que a medida que las diferencias crecen la magnitud del efecto se hace cada vez más grande.

Las fórmulas concretas, cuándo se utilizan, y cómo se interpretan lo indicaremos más adelante.

La familia de las correlaciones

Existe un segundo grupo de estimadores del tamaño o magnitud del efecto que se centran en la fuerza de la asociación entre variables y a él pertenecen toda la gama de coeficientes de asociación y/o correlación (r de Pearson, rho de Spearman, el coeficiente de determinación, etc.) agrupados bajo la denominación de ‘familia r del tamaño del efecto’.

Uno de los coeficientes más conocidos en estadística es la r de Pearson, también llamado coeficiente de correlación producto–momento. Se calcula cuando tratamos de establecer el grado de asociación entre dos variables medidas en escala continua o de razón; para variables de intervalo se utiliza el coeficiente de correlación por rangos de Spearman (rho), existiendo un gran número de coeficientes (el Biserial–puntual, la Q de Yule, etc.) que variarán en función de la combinación de la escala de las variables utilizadas.

En todos los coeficientes de asociación referidos, los valores asumibles oscilan entre –1 y +1, siendo el valor cero expresión de la ausencia de asociación, y aumentando el grado o magnitud de la asociación entre las variables a medida que se aproximan al valor unidad; el signo positivo o negativo informará sobre el sentido de la asociación. De este modo, un coeficiente de correlación igual a 1 (ó –1) indica que para cada valor de la variable X le corresponde un valor de la variable Y, existiendo, por tanto, una asociación perfecta. Otra forma de estimar el grado de asociación o magnitud del efecto es a partir del coeficiente de determinación R². Este se calcula elevando al cuadrado el coeficiente de correlación y expresa el porcentaje de varianza conjunta entre las variables consideradas.

La familia de las razones

EL tercer grupo de estimadores de la magnitud del efecto lo constituyen los Odds ratio (OR) y el Riesgo relativo (RR).

En el área de investigación biomédica existe todo un desarrollo de técnicas epidemiológicas que se han puesto al servicio de la evaluación terapéutica. Los diseños clásicos (cohortes, diseños de intervención, ensayos clínicos) se basan en la comparación de dos grupos diferenciados en función de la exposición o no a un factor ‘causal’ en los cuales se valora el desenlace de una determinada respuesta (salud–enfermedad, éxito–fracaso terapéutico, etc.).

Práctica científica y Magnitud del efecto

En la sexta edición de su Manual de Publicaciones, la American Psychological Association (APA) identifica la "falla en no informar los tamaños del efecto" como uno de los principales defectos observados en los manuscritos enviados. Al aplicar estadísticas inferenciales, se sugiere considerar la potencia estadística asociada a las pruebas de hipótesis. Tales consideraciones se relacionan con la probabilidad de rechazarlas correctamente, dado un nivel alfa particular, tamaño del efecto y el tamaño de muestra. En ese sentido, se solicita de forma rutinaria proporcionar evidencia de que el estudio tiene suficiente poder para detectar efectos de interés sustantivo. También se pide rigurosidad al discutir el papel desempeñado por el tamaño de la muestra en los casos en que no se rechaza la hipótesis nula (es decir, cuando se desea argumentar que no hay diferencias), cuando se prueban varios supuestos subyacentes al modelo estadístico adoptado (por ejemplo, normalidad, homogeneidad de varianza, homogeneidad de regresión) y en el ajuste del modelo.

Alternativamente, se sugieren cálculos de los correspondientes intervalos de confianza resultantes para justificar conclusiones sobre los tamaños del efecto -por ejemplo, que algún efecto sea insignificantemente pequeño- (APA, 2007; Brand, Bradley, Best, & Stoica, 2008).

Del mismo modo, en sus normas para la presentación de informes, la Asociación Estadounidense de Investigación Educativa (AERA) recomienda que los informes de resultados estadísticos deben ser acompañados por un tamaño del efecto y "una interpretación cualitativa del tamaño del efecto” (AERA, 2006).

Algunas reflexiones de Cohen en relación al tamaño del efecto

Cohen (1988) toma un ejemplo para reflexionar sobre la presencia o ausencia o medida de un efecto en la relación entre variables. Si se realizara un estudio para determinar si existe una diferencia de género en la incidencia de esquizofrenia paranoide, el investigador podría extraer una muestra de pacientes con ese diagnóstico de la población relevante y determinar la proporción de varones. La hipótesis nula que se pondría a prueba sería que la proporción de la población de hombres es 1/2, un valor específico. Además, podríamos decir que el tamaño del "efecto" del género en la presencia del diagnóstico es cero.

Podríamos, como ejemplifica Cohen en su trabajo, dar toda una serie “hipótesis nulas” en las que las diferencias planteadas por dichas hipótesis sean justamente que no hay ninguna diferencia. En cambio, cuando hablamos de “tamaño del efecto” se señala en qué medida, en qué grado la hipótesis nula es rechazada. En qué grado el fenómeno se encuentra presente en la población. Cuando la hipótesis nula es verdadera, entonces queremos significar que el tamaño del efecto debe ser cero. Sin embargo, cuando es falsa, determinar en qué medida, en qué grado lo es, es dar cuenta del tamaño del efecto (Cohen, 1988). Cuanto mayor sea este valor, mayor es el grado en que se manifiesta el fenómeno en estudio.

Así, en términos del ejemplo anterior:

Si el porcentaje de varones en la población de pacientes psiquiátricos con diagnóstico de esquizofrenia paranoide es del 52%, y el efecto es medido como una desviación del hipotético 50%. El tamaño del efecto será de 2%, si fuera de 60%, el tamaño del efecto será del 10%, es decir, más grande.

Sin embargo, resulta evidente que si otros estudios tratan de otras temáticas medidas en otras unidades va a ser problemática la comparación.

Es claramente deseable reducir esta diversidad de unidades en la medida de lo posible, en consonancia con el uso actual por los científicos del comportamiento o del área implicada. Un tamaño del efecto aplicable a diversos temas de investigación y modelos estadísticos utilizados en su evaluación, serían el ideal (Cohen, 1988).

En tal sentido el autor prepara al lector para incluir la estandarización del tamaño del efecto, la relación entre los distintos indicadores del tamaño del efecto y finalmente los criterios generales para la interpretación de los resultados.

La d de Cohen para la diferencia de medias a nivel de población

La necesidad de un número "puro", libre de sus unidades se logra estandarizando el tamaño del efecto bruto expresado en la unidad de medida de la variable dependiente (de resultado) dividiéndola por la desviación estándar (común) de las medidas en sus respectivas poblaciones:

 

 

 

Donde  es el tamaño del efecto (estandarizado) en la población, m_A es el promedio del grupo A en la población, m_B es el promedio del grupo B en la población, σ es la desviación estándar en la población.

En síntesis, no es suficiente con identificar la ocurrencia de cierto efecto, se requiere adicionalmente determinar su magnitud o tamaño (Cohen, 1992). Con tal propósito se han desarrollado diversas técnicas formales que permiten cuantificar el tamaño del efecto para diversas pruebas estadísticas habituales en la investigación psicológica como son, por ejemplo, la prueba t, el análisis correlacional r, y el análisis de varianza, entre otras (Cohen, 1988).

 

d de Cohen para diferencia de medias a partir de dos muestras (independientes)

 

Hasta ahora hemos hablado de un tamaño del efecto (para diferencia de medias) en una población.

Ahora bien, si se desea trabajar con muestras el cálculo del desvío conjunto sigue las siguientes formas:

d de Cohen

 

g de Hedges (corrección para

muestras pequeñas)

 

En el caso de g luego se ajusta de la siguiente manera (Hedges, 1981):

 

 ,

 

donde, 

En definitiva, la g ajustada estima la diferencia entre las medias de los grupos y estandariza dicha diferencia dividiéndola entre la desviación típica unificada de los dos grupos, con lo que el procedimiento aporta un parámetro tipificado (puntuación z), al que finalmente se le elimina el sesgo derivado del tamaño muestral. Así, este parámetro expresa un valor tipificado que en última instancia es de gran utilidad ya que permite inferir mediante la tabla de la curva normal el porcentaje de casos que un grupo deja por debajo del promedio del otro grupo. Como contrapartida, es necesario el cumplimiento de los supuestos de normalidad y homocedasticidad, especialmente con tamaños muestrales pequeños (por ejemplo, menos de 30 observaciones por grupo) (Pardo & San Martín, 1994).

Sin embargo, cuando el estudio apunta a la diferencia entre grupos de casos y controles, se suele utilizar como desvío estandarizado el que corresponde al grupo de control. Se trata en este caso de la Δ (delta) de Glass (Glass, McGaw, & Smith, 1981).

Como sea, las diferencias en el cálculo de estas distintas formas de tamaño del efecto suelen ser muy pequeñas y poco notorias, especialmente cuando las muestras son mayores a 30 casos.

La magnitud del efecto es simplemente una manera de cuantificar la efectividad de una particular intervención, relativa a alguna comparación. Es fácil de calcular y entender, y puede aplicarse a algún resultado medido en educación, economía, salud o ciencias sociales. Este concepto nos permite movernos más allá de la simple pregunta "¿el método A es efectivo o no? a una más sofisticada como "¿Qué tan bien funciona el método A en relación al método B? Más aún, al poner énfasis en el aspecto más importante de una intervención -la magnitud del efecto- más que en su significancia estadística (que pone en conflicto a la magnitud del efecto y el tamaño de la muestra), promueve un enfoque más científico a la acumulación de conocimientos. Por estas razones, es una herramienta importante para reportar e interpretar la efectividad de una condición específica o para describir las diferencias (Coe & Merino Soto, 2003).

También para Coe y Merino Soto se debe destacar que el uso de la palabra “efecto” sería algo inadecuado ya que efecto haría alusión a una relación causal entre las variables cosa que como se puede observar en muchos casos (estudios no experimentales o correlacionales) no se verifica. Aun así, dejamos señalado que es de uso habitual este término, pero evidentemente en muchos casos en un sentido genérico y no específico.

Otro aspecto ya señalado es que se trata de una medición sin unidades por lo cual permite, haciendo las salvedades y cuidados del caso, incorporar distintos estudios en lo que se denomina meta-análisis.

Para obviar estos problemas, o al menos para minimizarlos e interpretar mejor los resultados, una de las nuevas técnicas que se van imponiendo es calcular la magnitud o tamaño del efecto. Aquí la denominaremos tamaño del efecto (no hay unanimidad ni en los términos, ni en los símbolos utilizados). La expresión efecto se refiere obviamente al resultado de un tratamiento experimental, pero se la utiliza en los diseños más laxos en términos de variable predictora o factor como un simple contraste de medias. El tamaño del efecto se ha explicado de diversas maneras: nos dice cuánto de la variable resultado o dependiente se puede controlar, predecir o explicar por la variable factor o independiente  o en qué grado la hipótesis nula es falsa (Cohen, 1988); en definitiva el tamaño del efecto, como la misma palabra tamaño expresa, nos va a permitir hablar de magnitudes, de diferencias grandes o pequeñas y consiguientemente de la relevancia práctica o clínica de la diferencia encontrada (Morales Vallejo, 2012).

 

d de Cohen,  r de Pearson y t de Student

 

Ya hemos hablado de distintas familias de estimadores de los tamaños de efecto. Ahora toca comenzar a relacionar: de acuerdo con Cohen (1988) r (estimada) y d pueden ser relacionadas en determinadas condiciones según la siguiente fórmula:

 

 

O también podemos obtener r (estimada) en función de t -Rosnow y Rosenthal en Field (2013)-:

 

 

 

En Cohen (1988) podemos observar también la relación entre d y t a partir de las siguientes fórmulas:

 

 

 

 

 

Estas fórmulas permiten relacionar la t de Student, la d de Cohen y la r de Pearson. De modo que podemos también comenzar a establecer relaciones entre los indicadores a fin de facilitar la interpretación.

El intervalo de confianza para la d de Cohen

En cuanto a los intervalos de confianza de la d de Cohen encontramos en Nakagawa y Cuthill (2007) la siguiente ecuación que aproxima los intervalos de confianza para la d de Cohen:

 

 

 

O la siguiente para la corrección de Hedges:

 

 

Las fórmulas (10) y (11) pueden ser utilizadas para aproximar los intervalos de confianza. También es posible hallar otras fórmulas de aproximación que brindan valores muy similares hasta el nivel de centésimas. Por ejemplo, una fórmula para calcular el intervalo de confianza que proviene de Hedges y Olkin (1985, p. 86 en Coe & Merino Soto, 2003). Si la estimación del tamaño del efecto en la muestra es d, se distribuye normalmente, con una desviación estándar igual a:

 

 

 

Es decir, muy similar a la fórmula señalada por Hedges (Hedges, 1981).

Aunque aparentemente el modo más sencillo de obtener todos los valores es estandarizar la variable resultado o dependiente con cualquier programa estadístico y obtener tanto la d de Cohen como sus intervalos a partir de realizar un test de Student con dicha transformación. Debemos recordar que la d de Cohen es una diferencia estandarizada pero su cálculo presenta diferencias, por lo que dicho cálculo será solamente una aproximación, aunque frecuentemente muy buena. Las diferencias, en general pequeñas como ya fue señalado, son debidas a que la desviación en torno a la media total de las dos muestras, será levemente diferente si se ponderan las desviaciones en torno de cada una de las medias de los grupos.

Estas aproximaciones son mejoradas significativamente con la teorización de la distribución t no central (Algina, Keselman, & Penfield, 2005). Es que cuando la hipótesis nula no es rechazada, la distribución t de Student explica las variaciones muestrales (a igual grado de libertad). Sin embargo, cuando la alternativa es aceptada debe ser teorizada una nueva distribución de las muestras que siguen la siguiente distribución:

 

 , (Cousineau & Laurencelle, 2011)

 

En la que Z es una variable aleatoria normalmente distribuida con varianza unitaria y media cero, y V es una variable aleatoria distribuida de Chi-cuadrado con ν grados de libertad que es independiente de Z, y µ una variable aleatoria no central distribuida en t con ν grados de libertad y parámetro de no centralidad μ ≠ 0.

En Angina y Keselman (2005) observamos que:

 

 

 

Lambda representa el parámetro de no centralidad, d_s  la d de Cohen, n_a y n_b, la cantidad respectiva de casos muestrales.

Este es un artículo de divulgación que no tiene la pretensión de exponer en profundidad el conjunto de las técnicas que estamos ilustrando. Los cálculos están facilitados por diversos programas y calculadores en red. Se destacan los trabajos de Michael Smithson quien provee un programa en SPSS para el cálculo del tamaño de efecto (d de Cohen, F y Chi²) y sus respectivos intervalos de confianza. Una modificación de este trabajo puede ser hallada en la página de Wuensch Karl (http://core.ecu.edu/psyc/wuenschk/SPSS/SPSS-Programs.htm) (Wuensch's SPSS Links Page, 2019) también para SPSS y los calculadores de Geoff Cumming que pueden ser fácilmente hallados en la red (https://thenewstatistics.com/itns/) (Introduction to New Statistics, 2019).

Muchas veces los supuestos de normalidad y homocedasticidad no se cumplen. Se ha formulado la utilización de medias aritméticas y desvíos estándar basados en transformaciones de medidas de posición como en el caso de Wan (Wan, Wang, Liu, & Tong , 2014) y Hozo (Hozo, Djulbegovic, & Hozo, 2005) para resolver este problema. Si bien puede ser de utilidad en algunos casos, este abordaje ha sido cuestionado. Ver al final del trabajo el apartado sobre abordaje no paramétrico.

La interpretación del tamaño del efecto

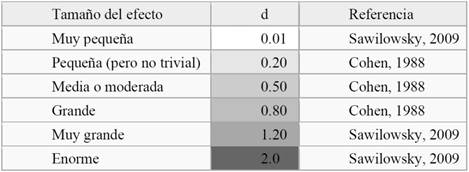
Cohen nos ofrece una forma de interpretar los tamaños de efecto. Sin embargo, Sawilowsky (2009) amplía la descripción de Cohen del siguiente modo:

 

Tabla 2. Interpretación de la d de Cohen

 

Estos valores fueron pensados especialmente para el cálculo de las muestras dado un α (error de tipo I) y un β (Error de tipo II) determinados, es decir, como puntos de partida a partir de los cuales obtener otros valores a partir de tamaños de efecto pequeños, medianos o grandes. Se plantean como una orientación para la interpretación. Un tamaño de efecto pequeño, por ejemplo, es un valor en torno a 0,2.

Sin embargo, aquí se debe ser cuidadosos al trabajar con los tamaños de efecto. Cohen afirmó que estos valores de interpretación deben ser considerados en cada escenario de investigación (1988). Ya que en cada ámbito esto puede cambiar de modo sustancial. Por ejemplo, un muy pequeño efecto en un tratamiento capaz de salvar vidas puede ser considerado un efecto importante de por sí, y porque puede evidentemente abrir las puertas a nuevas investigaciones. Por el lado contrario, podemos hallar tamaños de efecto medianos o incluso grandes según estas categorías de interpretación, pero que pueden carecer de importancia teórica, práctica o clínica.

Un tamaño del efecto es exactamente equivalente a un puntaje Z de una distribución normal. Por ejemplo, un tamaño del efecto de 0,8 significa que el puntaje de la persona promedio en el grupo experimental (o de comparación) es 0,8 (Coe & Merino Soto, 2003, pág. 150). Esto es muy importante porque es posible determinar el solapamiento de las dos distribuciones y por lo tanto los resultados pueden ser analizados en términos de sus respectivas probabilidades en términos de percentiles.

La interpretación del tamaño del efecto depende generalmente del presupuesto de que los valores de las distribuciones comparadas sean normales y con las mismas desviaciones estándar. Si estos presupuestos no pueden ser sostenidos, lo recomendable es realizar pruebas que no dependan de tales presupuestos, como las no paramétricas.

Medida de creencia en la hipótesis nula y alternativa: factor de Bayes

Uno de los grandes problemas que genera el test de hipótesis es que no nos informa acerca de la probabilidad de que la hipótesis nula sea cierta, o bien de su recíproca, la probabilidad de que la hipótesis alternativa sea cierta. Nos informa solamente si nuestros datos son compatibles con un riesgo de cometer un error de tipo I (por ejemplo, con una significación menor a 0,05), o bien, si no podemos rechazar la nula simplemente no podemos afirmar nada más que el poder de la prueba con la que hemos trabajado. Es decir, 0,8 si la prueba se hallaba en los estándares esperados.

Es aquí donde la estadística bayesiana viene a dar su contribución a la prueba que hemos realizado. El denominado factor de Bayes nos informa cuán probable es, de acuerdo a nuestros datos, tanto la hipótesis nula como la alternativa (Jeffreys, 1961). En particular muchas veces nos hallamos interesados en demostrar la equivalencia de dos grupos, tratamientos, etc. En estos casos nos interesa particularmente centrarnos en la hipótesis nula y su particular probabilidad de certeza (Morey & Rouder, 2011).

El desarrollo de Jeffreys de una prueba de hipótesis bayesiana fue motivado en parte por su convicción de que el uso de la significación p clásica es un absurdo (Jeffreys, 1961).

 

Se deriva del teorema de Bayes la siguiente fórmula que va a conducir la lógica de construcción bayesiana:

 

 

 

El factor de Bayes puede ser calculado en base a la siguiente fórmula (Faulkenberry, 2018):

 

  , con una forma muy similar en (Bolstad, 2007).

 

También es posible relacionar la t de Student con el Factor de Bayes del siguiente modo:

,  (Faulkenberry, 2018).

 

Donde n es el número de casos en la muestra, t es la t de Student, y gl los grados de libertad.

 

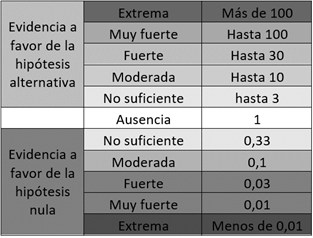
El factor de Bayes puede ser interpretado de acuerdo a la siguiente tabla:

 

Tabla 3. Interpretación del factor de Bayes

 

Este factor nos va a permitir indicar, de acuerdo a nuestro estudio, con cuánta evidencia contamos para afirmar nuestras hipótesis nula y alternativa respectivamente (Quintana & Williams, 2018; Hoekstra, Monden, van Ravenzwaaij, & Wagenmakers, 2018). Aquí, en contraposición al test de hipótesis, que tiende a dicotomizar los hallazgos, vamos a cuantificar la probabilidad de las evidencias a favor de las hipótesis (nula y alternativa) (Hoekstra, Monden, van Ravenzwaaij, & Wagenmakers, 2018).

Ahora bien, observando la fórmula del factor de Bayes depende también de la distribución a priori. La explicación de estos aspectos excede los límites de este trabajo. Sin embargo, esta distribución a priori puede ser considerada como no informativa dando por resultado una perspectiva más conservadora en cuanto a la aceptación de la hipótesis alternativa -Método de Rouder para el cálculo del factor de Bayes con distribución previa no informativa- (Morey & Rouder, 2011; Rouder, Speckman, Dongchu, & Iverson, 2009; Marsman & Wagenmakers, 2017).

En cuanto a la distribución a priori no informativa ver más detalles en el trabajo de Meng-Yun según el cual, si no contamos con información previa, es necesario especificar una distribución previa que no influya en la distribución posterior y "dejar que los datos hablen por sí mismos" (2013).

Los programas estadísticos (tal como el Jasp) por default utilizan una distribución de Cauchy (medida en una  escala de “r”) centrada en 0 y un valor intercuartil de 0,707 si uno espera un valor del tamaño  del efecto bajo como 0,2 o alto como 0,8. Si uno esperara valores más extremos esto puede ser modificado (Gronau, Ly, & Wagenmakers, 2018).

Meta-análisis

Ahora bien, puede ocurrir, que se encuentren estudios concordantes y discordantes en diversa medida. Muchos estudios podrán variar por razones simplemente estadísticas y entonces, en el mejor de los casos, la variabilidad que se observe entre los estudios dependerá “exclusivamente” del azar. Obviamente, muchas veces esas variaciones van a depender de otros factores que habrá que dilucidar para avanzar en el conocimiento de lo que se está estudiando.

El propósito del meta-análisis “es la integración de los resultados dispersos en múltiples estudios en los que se ponen a prueba una misma hipótesis, es decir, se trata de un análisis conjunto de otros análisis realizados anteriormente” (Macbeth, Cortada de Kohan, & Razumiejczyk, 2007).

El meta-análisis se refiere a la síntesis estadística de resultados cuantitativos de dos o más estudios. El meta-análisis debe reservarse para los resultados de estudios que se consideran suficientemente similares desde un punto de vista clínico y metodológico (estudios homogéneos). Si los estudios son heterogéneos desde un punto de vista clínico o metodológico, entonces no está claro si es apropiado sintetizar los estudios respectivos en un meta-análisis. Cualquier meta-análisis en el que los estudios sean heterogéneos desde un punto de vista clínico o metodológico requerirá una justificación sustancial por parte de los autores. La heterogeneidad clínica se refiere a las diferencias entre los estudios con respecto a los participantes, las intervenciones, los comparadores, los entornos y los resultados. La heterogeneidad metodológica se refiere al diseño del estudio y la calidad metodológica de los estudios (riesgo de sesgo) (Aromataris & Munn Z. (Editors), 2017).

Esencialmente el meta-análisis trata de determinar el valor más probable de tamaño de efecto a partir de los tamaños de efectos de estudios particulares.

Si bien no profundizaremos en la materia, el protocolo de revisión debe especificar entre otros los siguientes detalles:

Objetivos del meta-análisis

Modelo de meta-análisis (modelo de efectos fijos o modelo de efectos aleatorios) y su justificación,

Tamaño del efecto a utilizar (d de Cohen, OR, RR, etc.),

Método aplicado y justificación

Los procedimientos de prueba estadística utilizados para la exploración de la heterogeneidad estadística y las reglas utilizadas para la interpretación de los resultados,

Indicador estadístico utilizado para la cuantificación de la heterogeneidad estadística (como I²) y las reglas utilizadas para la interpretación de los resultados, y

Análisis de subgrupos planificados previamente y su justificación (clara descripción de los grupos que se van a comparar) (Aromataris & Munn Z. (Editors), 2017).

Uno de los principales objetivos del meta-análisis es dar cuenta de la heterogeneidad presente en los estudios. Si esta heterogeneidad es grande, evidentemente estará significando que estamos juntando peras con manzanas. Y deberá por lo tanto reenviar al investigador al análisis de los estudios incorporados en el meta-análisis.

Una prueba que puede ser utilizada es la Q de Cochran la cual se basa la suma de las desviaciones cuadráticas entre el resultado individual de cada estudio y el resultado global, ponderadas por el mismo peso con el que cada resultado interviene en el cálculo global:

 

 

 

La Q de Cochrane sigue una Chi² con k-1 grados de libertad. Sin embargo “el empleo de esta prueba no está exento de problemas, ya que si el número de estudios es pequeño su capacidad para detectar heterogeneidad es muy baja… por el contrario, cuando el meta-análisis combina gran número de estudios, el resultado puede ser estadísticamente significativo incluso cuando la magnitud de la heterogeneidad no sea de relevancia clínica” (SEH-LELHA, 2003).

Por este motivo se ha propuesto otro índice denominado I², este parámetro indica la proporción de la variación entre estudios respecto de la variación total, es decir la proporción de la variación total que es atribuible a la heterogeneidad, es realmente un indicador de inconsistencia en la heterogeneidad:

 

  (Borenstein, Hedges, Higgins, & Rothstein, 2009, pág. 117)

 

Donde Q es la Q de Cochrane, y gl representan los grados de libertad.

Los umbrales para la interpretación de I² pueden ser engañosos, ya que la importancia de la inconsistencia depende de varios factores. Una guía aproximada de interpretación es la siguiente (Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0, 2011):

 

0% a 40%: puede no ser importante;

30% a 60%: puede representar heterogeneidad moderada;

50% a 90%: puede representar heterogeneidad sustancial;

75% a 100%: heterogeneidad considerable.

 

Uno de los grandes problemas que debe afrontar un meta-análisis es el del sesgo de publicación, según Letón Molina y Pedromingo Marino (2001) (en Macbeth, Cortada de Kohan, & Razumiejczyk, 2007) este sesgo se debe a que “no todas las investigaciones, más allá de su calidad científica, poseen la misma probabilidad de ser publicadas. Los estudios que obtuvieron resultados estadísticamente significativos logran más fácilmente la publicación… Se cuenta con muchos estudios publicados que presentan resultados significativos, no así con resultados desfavorables”

Entonces evidentemente se corre el grave riesgo de no incluir estudios que no resultaron estadísticamente significativos según el test de hipótesis. El sesgo de publicación cobra la forma concreta de una sobreestimación del tamaño del efecto (Brand, Bradley, Best, & Stoica, 2008).

Rosenthal sugirió evaluar el potencial de sesgo de publicación para haber influido en los resultados de un meta-análisis calculando el 'N a prueba de fallas', el número de estudios 'negativos' adicionales (estudios en los que el efecto de la intervención fuera cero) que serían necesarios aumentar el valor de p para el meta-análisis por encima de 0,05 (en Higgins J.P.T., 2011 y Borenstein, Hedges, Higgins, & Rothstein, 2009).

La estimación de N a prueba de fallas depende en gran medida del efecto de intervención medio que se supone para los estudios no publicados. El N de seguridad (Fail-safe N) representa concretamente el número de muestras con tamaño de efecto 0 que deberían obtenerse para hacer que nuestro efecto calculado se haga 0 (Iyengar & Greenhouse, 1988).

Esta apretada síntesis del tema nos servirá de base para comprender los resultados que obtengamos en nuestros estudios y sobre los que nos ocuparemos en un próximo artículo. Quienes deseen profundizar en estos temas sugerimos la lectura del libro de Borenstein, Hedges, Higgins, & Rothstein (2009), o más recientemente el de Cooper, Hedges, & Valentine, (2019).

Métodos no paramétricos

Cuando nosotros nos disponemos a realizar una prueba de hipótesis de la diferencia entre dos medias independientes con una prueba t de Student consideramos ciertos supuestos: normalidad y homogeneidad de la varianza. Cuando estos no se cumplen existe la tendencia a la utilización de técnicas robustas para la prueba de hipótesis. Estas en general son adecuadas para la prueba de hipótesis, incluso cuando se comprueban pequeñas violaciones de los supuestos, pero no lo son en relación al tamaño de efecto. La d de Cohen en particular, es influenciada por la heterogeneidad de las varianzas (Grissom & Kim, 2012; Algina, Keselman, & Penfield, 2005; Wilcox, 2018).

El requerimiento de la realización de estimaciones de tamaño de efecto conlleva entonces un problema que debe ser afrontado. Es por ello que sugerimos acompañar a las pruebas de hipótesis basadas en la t de Student, y obviamente, en aquellos casos donde los supuestos no pueden ser alcanzados debido a la naturaleza de las variables -es decir, rangos y ordinales-, la realización de pruebas no paramétricas y tamaño de efecto asociado.

Se han propuesto en este sentido varios estadísticos. Recordemos que no existe consenso en la utilización de un único estadístico para el caso de la diferencia de muestras independientes, como en el caso paramétrico, para el que contamos con la t de Student para la prueba de hipótesis y la d de Cohen (o una de sus variantes) para el tamaño de efecto correspondiente. Pero existe una familia de test basados justamente en los rangos de las variables que pueden ser utilizados para los fines de la comparación de los grupos. Nótese que una vez que nos alejamos de los supuestos paramétricos e igualdad de las varianzas ya no podemos seguir hablando estrictamente de diferencia de medias aritméticas (ni en general de medianas). Las diferencias que tratan de captar estos test apuntan más allá de sus diferencias de localización, como es el caso de las medias aritméticas.

Muchas de las denominadas pruebas no paramétricas se basan en la naturaleza ordinal de las variables o en transformaciones de los valores originales (cuando su de nivel de medición es de intervalos o de razón) hacia categorías ordinales. Tienen en común un aspecto favorable. Es que los rangos eliminan los casos extremos de nuestras variables, tendiendo muchas veces a que nuestras distribuciones sean algo más simétricas, y esto es algo realmente bueno, pero este don tiene un precio: se pierde algo de información en relación a las diferencias entre las puntuaciones originales. En relación a estas medidas se suele considerar que ellas tienen menor poder para captar significación estadística y tamaño de efecto que sus contrapartes paramétricas. Pero como afirma Field esto no es siempre así porque justamente toda la capacidad de las pruebas paramétricas se desvanece en tanto no se alcancen los supuestos para su aplicación (2013).

Estas pruebas son denominadas “libres de suposiciones” porque requieren menos -supuestos- que las denominadas paramétricas. Pero considerarlas “libres” parece algo exagerado cuando muchas veces, como en el caso del que nos ocuparemos a continuación, requieren “igual forma”, más allá de la distribución normal.

Para el propósito de la comparación de dos grupos de valores que no pueden ser considerados como paramétricos y de igual varianza, ha cobrado gran desarrollo teórico y práctico el denominado coeficiente U de Mann-Whitney. Prevenimos aquí al lector por problemas en la denominación del estadístico. El test de suma de rangos de Wilcoxon (1945) y el test de Mann-Whitney (1947) son equivalentes por lo que algunos prefieren la denominación Wilcoxon-Mann-Whitney (WMW).

La siguiente ecuación relaciona ambos coeficientes:

 

 (Juárez Hernández, Sotres Ramos, & Matuszewski, 2001).

 

W es el coeficiente de suma de rangos de Wilcoxon,  y  son los que corresponden a las ecuaciones que se presentan a continuación (21 y 22).

El estadístico U de Mann-Whitney viene dado por: U = mínimo (U₁,U₂), siendo:

 

 

 

 

Donde  es el tamaño de la muestra del grupo 1,  es el tamaño de la muestra del grupo 2,  es la suma de los rangos del grupo 1 y  es la suma de los rangos del grupo 2.

En los casos en que n15, puede considerarse la aproximación a la normal por muestra suficientemente grande (teorema central del límite) al nivel de 0,05 de significación o n29 a 0,01 de significación (Grissom & Kim, 2012, pág. 144), por lo que es aplicable la siguiente aproximación a la normal para el cálculo de Z:

 

 

 

 

 

Esta es la fórmula (24) que en general encontramos en muchos libros. Sin embargo, como existen diferencias en las ecuaciones utilizadas en distintos softwares es conveniente señalar la fórmula completa, para el caso que existan empates, el cálculo del error de la normal estándar va a ser diferente:

 

 

 

con  

 

donde t es el número de observaciones empatadas en relación con un orden determinado (Blalock, 1994, pág. 274).

Existen otros estadísticos, que por razones de extensión no abordaremos en este trabajo. Nos referimos -especialmente- a la probabilidad de superioridad (PS), al estadístico CL (de difícil traducción al castellano: Common Language Effect Size), y al estadístico de medida de dominancia (conocido como delta de Cliff). Sin embargo, como ya hemos sugerido, la U de Mann-Whitney (o su equivalente W suma de rangos de Wilcoxon) son por lejos los más utilizados. Aunque obviamente no siempre resulte aconsejable su utilización y se requiera en determinadas situaciones evaluar la aplicación de otros coeficientes. Recordemos que los supuestos de la U de Mann-Whitney son que las mediciones sean independientes y que ambos grupos presenten la misma “forma”.

Seguidamente veremos para finalizar este apartado algunos de los tamaños de efecto que pueden ser utilizados acompañando la U de Mann-Whitney. Del mismo modo que en el caso de la prueba de hipótesis, no encontramos consenso en la aplicación concreta, por parte de los investigadores, en los coeficientes de tamaño de efecto. Su aplicación debiera ser obligatoria en los reportes a fin de que otros estudios puedan incluirlos en correspondientes meta-análisis. Por lo que el investigador deberá elegir el coeficiente que considere de acuerdo con su conocimiento en la materia y sus posibilidades de cálculo, evidentemente condicionadas por el software que utilice. Se aconseja que los resultados obtenidos a partir de estos coeficientes sean transformados a la métrica de la d de Cohen, en general comprendida por la mayor parte de los investigadores.

 

El primero de los tamaños de efecto para el caso de distribuciones no paramétricas, el más difundido, es el coeficiente r basado en el score de Z (Rosenthal 1991, en Field, 2013):

 

 

 

Para el cálculo del intervalo de confianza de r es posible utilizar la transformación Z de Fischer de acuerdo con:

 

 

 

Calculando los límites del intervalo en Z de acuerdo con

 

 

 

Y luego volviendo a transformar a r de acuerdo con:

 

 (Grissom & Kim, 2012, pág. 104; Cooper, Hedges, & Valentine, 2019, págs. 220-221).

El segundo de ellos, es el test de correlación biserial por rangos (rank biserial correlation) introducido por Edward Cureton en 1956 (Kerby, 2014) y reelaborado por Glass (1966) acompañando la prueba no paramétrica U de Mann-Whitney (Wilcoxon-Mann-Whitman) con el propósito de derivar una fórmula para el caso de la Rho de Spearman con una variable dicotómica (de naturaleza ordinal). Este estadístico no debe ser confundido con el test de correlación biserial por puntos que también puede ser utilizado como tamaño del efecto en los casos en que la variable dicotómica no sea continua por naturaleza (Grissom & Kim, 2012). Estos estadísticos son sensibles a las diferencias en los tamaños de las muestras comparadas.

 

   (Garret, 1983),

 

donde  representa el promedio de rangos del grupo p y  el promedio de rangos del grupo q.  es la desviación del conjunto de los datos,  p y q son las proporciones de cada grupo, e y representa la ordenada al origen de la distribución normal estándar para el valor que separa p y q.

Otra fórmula, más sencilla, obtenida por Wentd (Kerby, 2014) a partir de la U de Mann-Whitney es la siguiente:

 

 

 

Mientras que el error estándar puede ser calculado a partir de:

 (Garret, 1983), con las mismas indicaciones respecto a la ecuación (31) salvo que N hace referencia al total de las muestras y  representa el valor de la correlación biserial por rangos.

 

Finalmente, la tercera medida de tamaño de efecto sugerida es la propuesta por Alan Agresti, quien, continuando los trabajos de Clayton sobre odds ratios, y considerando su desarrollo en el marco de las medidas de asociación propuestas por Goodman y Kruskal, desarrolla un estadístico que denomina Odds Ratio Generalizado con la siguiente forma:

 (Agresti, 1980)

 

Este estadístico fue luego reformulado debido su dificultad para dar cuenta de los empates en las distribuciones del siguiente modo (Cumming, Churilov, & Sena, 2015):

 

 

 

Y su error estándar viene dado por:

 

 

 

Para transformar los resultados en términos de GenOR a d de Cohen es posible basarse en la fórmula del capítulo de Borenstein y Hedges en Cooper, Hedges, & Valentine (2019, pág. 234):

 

 

 

Este estadístico, a pesar de ser quizá el menos conocido de los desarrollados aquí, presenta un cálculo del error estándar realmente muy elegante. Debido a que los OR tienen la propiedad de ser simétricos en torno a 1 -facilitando su interpretación-, y su facilidad para transformarse en la d de Cohen se lo ha señalado como un estadístico semi-paramétrico.

Existen otra serie de estadísticos que pueden ser utilizados, y que se encuentran en discusión. Quienes deseen profundizar sobre estos temas sugerimos la lectura del libro de Grissom y Kim y, en general, el capítulo sobre tamaños de efecto escrito por Michael Borenstein y Larry V. Hedges del libro de Cooper y otros, ambos abundantemente citados en este trabajo.

CONCLUSIONES

Este trabajo ha intentado poner de manifiesto la necesidad de profundizar en los conocimientos y prácticas estadísticas en el caso de las diferencias de medias. Las pruebas de hipótesis o de significación estadística han prevalecido, en general, como las únicas para sostener hipótesis de investigación.

Aquí se ha subrayado la importancia de acompañar la toma de decisión estadística con otros coeficientes. Los tamaños de efecto deben ser informados siempre, y se tornan imprescindibles cuando se ha hallado significación estadística. Hablar de significación estadística de la diferencia -de medias o el estadístico que fuere- no informa en qué medida se produce un efecto. Podría por caso ser extraordinariamente pequeño, o por el contrario muy grande. Es decir, se trata de una información necesaria, pero insuficiente. 

Del mismo modo, un detallado análisis previo de la potencia de la prueba es necesario, y estamos obligados a informarla cuando no se halle significación estadística simplemente por el hecho de que pueda confundir la interpretación de los resultados sugiriendo una eventual ausencia de efecto cuando éste puede existir y no ser detectado debido a un deficiente poder de la prueba que hemos aplicado. De ser posible es necesario utilizar otras técnicas que den cuenta de la probabilidad de la hipótesis aceptada. El factor de Bayes parece ser una buena elección.

En el caso particular de la diferencia de medias independientes es necesario también comprobar los supuestos de las pruebas. Existe una tendencia a utilizar las pruebas paramétricas cuando pequeñas desviaciones de los supuestos se producen. En general esto no implica mayores problemas respecto a las pruebas de significación -a partir de la utilización de pruebas robustas-, pero son problemáticas en el caso de los tamaños de efecto. Por tal motivo es necesario acompañar las pruebas de significación con pruebas no paramétricas y sus correspondientes tamaños de efecto en tales circunstancias.

El investigador debe buscar el modo de dar a conocer la totalidad de los estudios realizados, y no solamente los que resultaron estadísticamente significativos. En esto también puede haber responsabilidad de las editoriales al “premiar” a los investigadores que obtengan resultados significativos. Esta es una “cultura” que tiende a aportar confusión y eventualmente conclusiones falsas. Meta-análisis bien realizados pueden colaborar con una puesta en común y aportar de modo importante al conocimiento científico. 

  Referencias bibliográficas.

AERA. (2006). Standards for reporting on empirical social science research in AERA publications. Educational Researcher, 36(6), 33-40.

Agresti, A. (1980). Generalized Odds Ratios for Ordinal Data. International Biometric Society, 36(1), 59-67.

Algina, J., Keselman, H. J., & Penfield, R. D. (2005). An Alternative to Cohen's Standarized Mean Differencie Effect Size: A Robust Parameter and Confidence Interval in the Two Independent Groups Case. Psychological Methods, 10(3).

APA. (2007). Manual of the American Psychological Association (APA) (Sixth ed.). Washington. DC.

Aromataris, E., & Munn Z. (Editors). (2017). Joanna Briggs Institute Reviewer's Manual. Retrieved from The Joanna Briggs Institute: https://reviewersmanual.joannabriggs.org

Blalock, H. M. (1994). Estadística social. México: Fondo de cultura económica.

Bolstad, W. M. (2007). Introduction to Bayesian Statistics. New Jersey: John Wiley & Sons, Inc.

Borenstein, M., Hedges, L., Higgins, J., & Rothstein, H. (2009). Introduction to Meta-Analysis. West Sussex: John Wiley & Sons, Ltd.

Brand, A., Bradley, M. T., Best , L. A., & Stoica, G. (2008). Accuracy of Effect Size Estimates from Published Psychological Research. Perceptual and Motor Skills, 106, 645-649.

Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0. (2011). Retrieved from https://handbook-5-1.cochrane.org/chapter_9/9_5_2_identifying_and_measuring_heterogeneity.htm

Coe, R., & Merino Soto, C. (2003). Magnitud del Efecto: Una guía para investigadores y usuarios. Revista de Psicología de la PUCP. Vol. XXI,, XXI(1).

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (Second ed.). New York: Lawrence Erlbaum Associates, Publishers.

Cohen, J. (1992). A Power Primer. Psychological Bulletin, 112(1).

Cohen, J. (1994). The Earth Is Round (p < .05). American Psychological Association, 49(12), 997-1003.

Cooper, H., Hedges, L. V., & Valentine, J. C. (2019). The Handbook of Research Synthesis and Meta-Analysis (3rd. ed.). New York: Russell Sage Foundation.

Cousineau, D., & Laurencelle, L. (2011). Non-central t distribution and the power of the t test: A rejoinder. Tutorials in Quantitative Methods for Psychology, 7(1).

Cumming, G. (2014). The New Statistics: Why and How. Psychological Science (Sage), 25(1).

Cumming, T. B., Churilov, L., & Sena, E. S. (2015). The Missing Medians: Exclusion of Ordinal Data from Meta-Analysis. Plos One.

Ellis, P. D. (2010). The Essencial guide to Effect Size. Cambridge: University Press.

Faulkenberry, T. J. (2018). Computing Bayes factors to measure evidence from experiments: An extension of the BIC approximation. Biometrical Letters.

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. London: Sage Publications Ltd.

Garret, H. E. (1983). Estadística en psicología y educación. Buenos Aires: Paidos.

Glass , G. V. (1966). Note on rank-biserial correlation. Educational and Phychological measurement, 26, 623-631.

Glass, G. V., McGaw, B., & Smith, M. L. (1981). Meta-analysis in social research. Newbury Park: Sage Publications.

Grissom, R. J., & Kim, J. J. (2012). Effect Sizes for Research: Univariate and Multivariate Application. New York: Routkedge.

Gronau, Q. F., Ly, A., & Wagenmakers, E.-J. (2018). Informed Bayesian T-Tests. Retrieved from https://arxiv.org/abs/1704.02479

Hedges, L. V. (1981). Distribution Theory for Glass's Estimator of Effect Size and Related Estimators. Journal of Educational Statistics, 6.

Higgins J. P. T., G. S. (2011). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 [updated March 2011]. Retrieved from The Cochrane Collaboration: www.handbook.cochrane.org

Hoekstra, R., Monden, R., van Ravenzwaaij, D., & Wagenmakers, E.-J. (2018). Bayesian reanalysis of null results reported in medicine: Strong yet variable evidence for the absence of treatment effects. PLoS ONE , 13(4), https://doi.org/10.1371/journal.pone.0195474.

Hoekstra, R., Monden, R., van Ravenzwaaij, D., & Wagenmakers, E.-J. (2018). Bayesian reanalysis of null results reported in medicine: Strong yet variable evidence for the absence of treatment effects. Plos One.

Hozo, S. P., Djulbegovic, B., & Hozo, I. (2005). Estimating the mean and variance from the median, range, and the size of a sample. BMC Medical Research Methodology, 5(13).

Introduction to New Statistics. (2019, 10). Retrieved from https://thenewstatistics.com/itns/

Ioannidis, J. P. (2005). Why Most Published Research Findings are False. PLoS Medicine, 2(8).

Ioannidis, J. P. (2014). How to make more published research true. PLoS Med, 11(10).

Ioannidis, J. P. (2016). Why Most Clinical Research Is Not Useful. PLoS Med, 13(6).

Iraurgi, I. (2009). Evaluación de resultados clínicos (II): Las medidas de la significación clínica o los tamaños del efecto. NORTE DE SALUD MENTAL(34), 94–110.

Iyengar, S., & Greenhouse, J. B. (1988). Selection Models and de File Drawer Problem. Statisticasl Science, 3(1).

Jeffreys, H. (1961). Theory of probability (3rd. ed.). New York, NY: Oxford University Press.

Juárez Hernández, B., Sotres Ramos, D. A., & Matuszewski, A. (2001). Distribución exacta de la estadística prueba tipo Mann-Whitney-Wilcoxon bajo violaciones a los supuestos estándar, para distribuciones uniformes continuas. Agrociencia, 35(2), 223-235.

Kerby, D. S. (2014). The simple difference formula: an approach to teaching nonparametric correlation. Comprehensive Psycology, 3(1).

Macbeth, G., Cortada de Kohan, N., & Razumiejczyk, E. (2007). El Meta-Análisis: La Integración de los Resultados Científicos. Evaluar, 7.

Marsman, M., & Wagenmakers, E.-J. (2017). Bayesian benefits with JASP. European Journal of Developmental Psycholog, 14(5), 545-555.

Meng-Yun , L. (2013). Bayesian Statistics. https://www.bu.edu/sph/files/2014/05/Bayesian-Statistics_final_20140416.pdf. Boston University School of Public Health.

Morales Vallejo, P. (2012, Octubre 3). El tamaño del efecto (effect size):análisis complementarios al contraste de medias. Retrieved 2019, from https://web.upcomillas.es/personal/peter/investigacion/Tama%f1oDelEfecto.pdf

Morey, R. D., & Rouder, J. N. (2011). Bayes Factor Approaches for Testing Interval Null Hypotheses. Psychological Methods.

Nakagawa, S., & Cuthill, I. C. (2007). Effect size, confidence interval and statistical significance: a practical guide for biologists. Biological Reviews, 82, 591-605.

Nunnaly , J. (1960). The Place of Statistics in Psychology. Educational and Psychological Measurement, XX(4).

Pardo, A., & San Martín, R. (1994). Análisis de datos en Psicología II. Madrid: Pirámide.

Pértegas Díaz, S., & Pita Fernández, S. (2003). Cálculo del poder estadístico de un estudio. Cad Aten Primaria, https://www.fisterra.com/mbe/investiga/poder_estadistico/poder_estadistico.asp, 59-63.

Quintana, D. S., & Williams, D. R. (2018). Quintana,Bayesian alternatives for common null-hypothesis significance tests in psychiatry: a non-technical guide using JASP. BMC Psychiatry, https://doi.org/10.1186/s12888-018-1761-4.

Rouder, J. N., Speckman , P. L., Dongchu , S., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16(2), Psychonomic Bulletin & Review.

Sawilowsky, S. S. (2009). New effect size rules of thumb. Journal of Modern Applied Statistical Methods, 8(2), 597 – 599.

SEH-LELHA. (2003). Heterogeneidad entre los estudios incluidos en un meta-análisis. Retrieved from Liga española para la lucha contra la hipertensión arterial: https://www.seh-lelha.org/heterogeneidad-los-estudios-incluidos-meta-analisis/

Wan, X., Wang, W., Liu, J., & Tong , T. (2014). Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range. BMCMedical Research Methodology, 14(135).

Wilcox, R. (2018). A robust nonparametric measure of effect size based on an analog of Cohen's d, plus inferences about the median of the typical difference. Journal of Modern Applied Statistical Methods, 17(2).

Wilson, D. B. (2020, 4 11). Campbell Collaboration. Retrieved from Practical Meta-Analysis Effect Size Calculator: https://campbellcollaboration.org/research-resources/effect-size-calculator.html

Wuensch's SPSS Links Page. (2019, 10). Retrieved from http://core.ecu.edu/psyc/wuenschk/SPSS/SPSS-Programs.htm

Ziliak, S., & McCloskey, D. N. (2008). The Cult of Statistical Significance. How the Standard Error Costs Us Jobs, Justice, and Lives. University of Michigan Press - Ann Arbor.

 

  Revista Interdisciplinaria de Economía Política está bajo una licencia de Atribución-NoComercial-SinDerivadas CC BY-NC-ND.