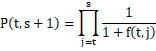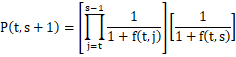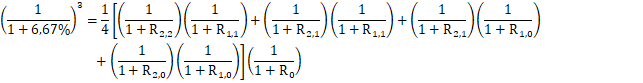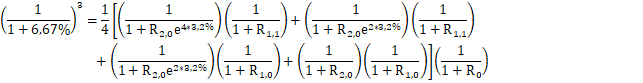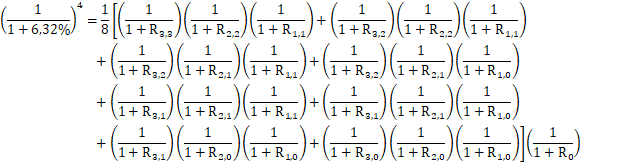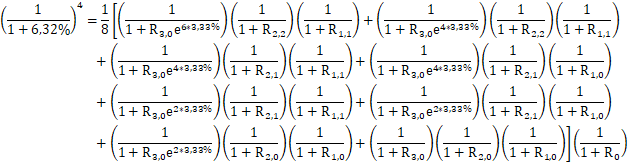- J.P. Morgan Services Argentina S.R.L.
RESUMEN
Palabras clave: Expectativas; Curva, emisiones, canje de deuda, árbol de tasas de interés y valuación derivados en pesos argentinos; Modelo Black, Derman y Toy.
ABSTRACT
Keywords: Expectations; Yield curve, issues, debt swap, interest rate tree and valuation derivatives in Argentine pesos; Black, Derman and Toy model.
INTRODUCCIÓN
El trabajo comienza con preliminares sobre tasas de interés, en particular, definición de la short rate a partir de la zero rate y de la forward rate. Luego, se detalla el modelo de Black, Derman y Toy (1990) de construcción del árbol de tasas de acuerdo a la información presente en el mercado. El documento procede con una aplicación del modelo al caso argentino. Para ello, en primer lugar, se construye la curva con los bonos seleccionados, luego se estima un modelo para poder obtener la tasa para cualquier duration y, en tercer lugar, se relevan los desvíos de la tasa BADLAR. Todos los datos son utilizados para la construcción de un árbol de tasas que permita valuar cualquier derivado de tasas en pesos. El trabajo cierra con observaciones de los resultados.
Preliminares sobre tasas de interés
Antes de especificar el modelo es necesario definir algunos conceptos. La nomenclatura y desarrollos utilizados en la presente sección se deben a Lin (2006).
Se define a la short rate en t como la tasa que capitaliza desde t a t+1. En símbolos:
|
( 1) |
Donde la zero rate ![]() es la tasa que capitaliza desde t a t+1 y se define como:
es la tasa que capitaliza desde t a t+1 y se define como:
|
( 2) |
Siendo ![]() el precio en t de un bono cupón cero que paga 1 en t+1.
el precio en t de un bono cupón cero que paga 1 en t+1.
La expresión anterior se deriva de la siguiente manera:
|
( 3) |
De manera general, se define a la zero rate ![]() como la tasa efectiva periódica equivalente a la tasa interna de retorno (TIR) de un bono
como la tasa efectiva periódica equivalente a la tasa interna de retorno (TIR) de un bono ![]() , es decir, un bono cupón cero en t que paga 1 en s, con
, es decir, un bono cupón cero en t que paga 1 en s, con ![]() . En símbolos:
. En símbolos:
|
( 4) |
La expresión anterior se deriva de la siguiente manera:
|
( 5) |
Además, se define a la short rate de la siguiente manera:
|
( 6) |
Donde la forward rate ![]() es la tasa definida en t que capitaliza desde t a t+1 y se define como:
es la tasa definida en t que capitaliza desde t a t+1 y se define como:
|
( 7) |
La expresión anterior se deriva de la siguiente manera:
|
( 8) |
De manera general, se puede definir a la forward rate ![]() como la tasa definida en t que capitaliza desde s a s+1. En símbolos:
como la tasa definida en t que capitaliza desde s a s+1. En símbolos:
|
( 9) |
La expresión anterior se deriva de la siguiente manera:
|
( 10) |
Se puede calcular el precio en t de un bono cupón cero que paga 1 peso en s ![]() de la siguiente manera:
de la siguiente manera:
|
( 11) |
Sobre el modelo de Black, Derman y Toy
El mencionado trabajo (Black et al., 1990) propone un modelo de tasas de interés que puede ser utilizado para valuar cualquier activo sensible a las mismas. El trabajo también ejemplifica su aplicación mediante la valuación de bonos del Tesoro de EEUU, calls y puts europeos sobre dichos instrumentos y la determinación del hedge ratio o delta de una opción europea sobre bonos, es decir, una medida de la cuantía de la variación de los precios de las opciones en respuesta a los cambios de precios de los bonos subyacentes.
El modelo tiene tres características principales:
- Su variable fundamental es la tasa de interés de corto plazo, es decir, la tasa de interés anualizada de un período. La tasa de corto plazo es el único factor del modelo y sus cambios impulsan todos los precios de los activos.
- El modelo toma como insumos una matriz de tasas de interés de largo plazo para varios vencimientos y una matriz de volatilidades de rendimientos para los mismos bonos. La primera matriz se conoce como la curva de rendimiento y la segunda como la curva de volatilidad.
- El modelo supone un mundo imaginario en el que los cambios en todos los rendimientos de los bonos están perfectamente correlacionados; los rendimientos esperados de todos los activos en un período son iguales; las tasas de interés de corto plazo en cualquier momento se distribuyen lognormalmente; y no hay impuestos ni costos de transacción.
El modelo de Black, Derman y Toy (BDT) propone considerar el proceso de las short rate como un random walk geométrico según la siguiente especificación:
|
( 12) |
Donde:
|
( 13) |
Se asume que las varianzas son determinísticas pero varían con el tiempo según la siguiente formulación:
|
( 14) |
Por lo tanto, la volatilidad queda definida como:
|
( 15) |
El resultado anterior se demuestra de la siguiente manera:
|
( 16) |
El árbol de tasas se arma utilizando la estructura temporal de tasas y volatilidades resultante de los precios de los bonos cupón cero del mercado y de manera tal que sea recombinante. Para el caso del modelo anteriormente especificado:
|
(17) |
Donde:
![]()
![]()
![]()
La fórmula se puede mostrar por recurrencia usando el supuesto de volatilidad establecido en ( 17).
Por recurrencia, comenzando desde la rama inferior del árbol, para el caso de j=1:
|
( 18) |
En el caso anterior partimos de la siguiente igualdad:
|
( 19) |
Para el caso de j=2:
|
( 20) |
Nuevamente, partimos de la siguiente igualdad:
|
( 21) |
Para el caso de j=3:
|
( 22) |
También partimos de la siguiente igualdad:
|
( 23) |
De esta manera, por recurrencia, llegamos a la especificación detallada en ( 17).
La tasa ![]() puede ser despejada para cada i (i=1,2,…,t) a partir de la igualdad de tasas antes desarrollada en ( 17):
puede ser despejada para cada i (i=1,2,…,t) a partir de la igualdad de tasas antes desarrollada en ( 17):
|
(24) |
Hay que tener en cuenta que la especificación del modelo anterior es válida en el caso de que los datos de mercado sean anuales. En otro caso, debido al hecho de que la volatilidad es proporcional a la raíz cuadrada del paso del tiempo, el algoritmo asume la siguiente forma:
|
( 25) |
Donde:
![]()
A modo de ejemplo, se reproduce un árbol de tasas para los primeros 4 períodos.
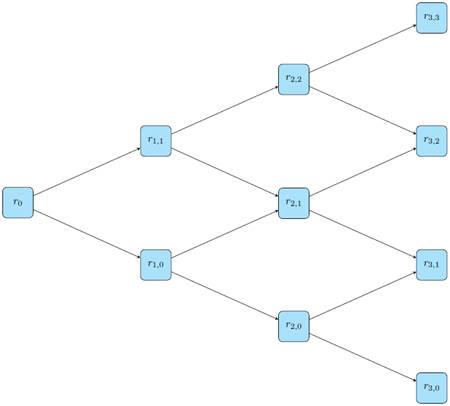
Fuente. Elaboración propia.
El modelo de BDT se enmarca dentro de una tipología de modelos que se conocen como de árbol o lattice, siendo otros grupos de modelos aquellos basados en las ecuaciones diferenciales estocásticas y simulaciones de Monte Carlo.
Las características generales de los modelos de árbol se pueden resumir, según Rebonato (1998), en: (i) todos los precios implícitos de los bonos coinciden con los precios del mercado; (ii) son una implementación en tiempo discreto de la condición que asegura ausencia de arbitraje; y (iii) son algoritmos eficientes.
Algunas de las características salientes del modelo de BDT son su popularidad en la industria, simplicidad de su calibración y la facilidad para interpretar sus resultados. En este último punto se diferencia del modelo de Ho y Lee (1986) en que, a pesar de estar basado en una idea de árbol, modela a partir de las tasas forward, con resultados menos intuitivos.
Además, el modelo de BDT no requiere especificaciones respecto de las preferencias en cuanto al riesgo de los inversores y asume, como ya se ha mencionado, un proceso estocástico para las short rate que impide tasas negativas y que, además, permite especificar la curva de volatilidades en términos porcentuales.
Los dos principales inconvenientes del modelo son: (i) incapacidad de incorporar condiciones donde el impacto de un segundo factor es relevante; y (ii) la imposibilidad de especificar la volatilidad de los rendimientos para diferentes maturities independientemente de la volatilidad futura de la short rate.
En cuanto a la necesidad de incorporar una correlación imperfecta entre las tasas implícitas en el modelo entonces otro tipo de modelo también sería más adecuado. Por ejemplo, pueden citarse los de Longstaff y Schwartz (1992), Heath et al. (1992) o Brennan y Schwartz (1982). En el caso de querer incorporar independientemente la volatilidad futura de la short rate y la estructura temporal de volatilidades, entonces el modelo de Hull y White (1990) sería más apropiado. Existen también los llamados modelos de tiempo homogéneo que podrían ayudar a controlar la evolución futura de la estructura temporal de la tasa de interés (Rebonato, 1998).
Aplicación al caso argentino
Los primeros objetivos son construir una estructura temporal de tasas de interés y una estructura temporal de volatilidades que nos permitan luego implementar el modelo BDT para el caso argentino.
En Argentina coexisten bonos muy heterogéneos, lo que lleva a la confección de estructuras temporales de tasas de interés dependiendo de la naturaleza de los instrumentos seleccionados. Es así como se pueden encontrar curvas de bonos en dólares o pesos, a tasa fija o variable, con o sin indexación y con distintos sistemas de amortización de capital (Más, 2008).
Para el presente trabajo se han seleccionado los bonos en pesos indexados con índice CER o a tasa variable BADLAR de las siguientes emisiones: (i) bonos canje reestructuración de deuda 2005; (ii) bonos canje reestructuración de deuda 2010; (iii) Bonte, Bogar y Bonos de consolidación emitidos en pesos durante la gestión de Martín Guzmán.
Las categorías (i) y (ii) antes detalladas se incluyen por dos razones. En primer lugar, son bonos con una maturity de largo plazo y nos permiten extender la estimación de la curva hacia adelante en el tiempo sin la necesidad de extrapolar. En segundo lugar, se supone en este trabajo que los bonos indexados en pesos resultantes de reestructuraciones de deuda no se volverán a reestructurar.
Dentro de esas categorías incluimos los siguientes instrumentos:
- DIP0
- DICP
- CUAP
- PAP0
- PARP
Dentro de la categoría (iii) se incluyen los siguientes títulos:
- TB21
- TX21
- TX22
Se excluyen los bonos TX23 y TX24, emitidos en el marco del canje de bonos llamado a licitación el día 16 de marzo del 2020 (Ministerio de Economía, 2020). También se excluye el bono del tesoro en pesos ajustado por CER 1,10% vencimiento 17 de abril de 2021 emitido en el canje de bonos llamado a licitación el día 8 de abril de 2020 (Ministerio de Economía, 2020). Los dos primeros se excluyen ya que al momento de la confección del presente trabajo no contaban con la suficiente liquidez en el mercado secundario como para ser incluidos, mientras que el último security todavía no fue licitado.
Las condiciones de emisión de dichos títulos pueden encontrarse en Bolsar (2020).
Siguiendo las recomendaciones de Más (2008), para el caso de economías con alta heterogeneidad en sus instrumentos, se ha decidido construir la curva de tasas utilizando los instrumentos arriba señalados y utilizando la duration (DUR) en lugar del plazo al vencimiento.
Para el cálculo de la duration y de la TIR de los instrumentos seleccionados se ha procedido a utilizar los datos provistos por el Instituto Argentino del Mercado de Capitales (IAMC) (2020). Todos los instrumentos se han valuado al día 6 de abril de 2020.
BONO |
TIR |
DUR |
ln(DUR) |
TB21 |
101,48% |
1,02 |
0,020 |
TX21 |
57,47% |
1,32 |
0,278 |
TX22 |
38,82% |
1,92 |
0,653 |
DIP0 |
18,88% |
5,44 |
1,693 |
DICP |
18,36% |
5,49 |
1,703 |
CUAP |
13,06% |
9,75 |
2,277 |
PAP0 |
13,03% |
10,30 |
2,332 |
PARP |
12,85% |
10,34 |
2,336 |
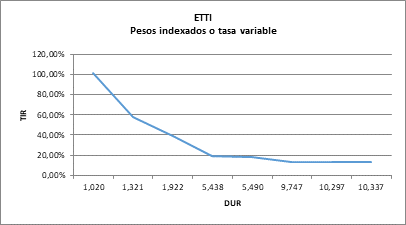
A partir de la curva, se puede realizar un ajuste de mínimos cuadrados ordinarios que permita predecir, para cualquier DUR, la TIR de mercado de los instrumentos con características similares. La regresión utilizada es el estándar utilizado en el mercado para la estimación de curvas de rendimientos (IAMC, 1998). El modelo estimado queda definido de la siguiente manera:
|
(26) |
Los detalles de la estimación pueden consultarse en el Apéndice I.
A partir del modelo, se puede estimar la TIR para momentos discretos del tiempo, en nuestro caso nos interesa estimar para intervalos mensuales. El resultado es una curva de rendimientos creciente.
DUR (años) |
ln(DUR) |
TEA estimada |
TEM equivalente |
1/12 |
-2,48 |
149,70% |
7,92% |
1/6 |
-1,79 |
129,16% |
7,15% |
1/4 |
-1,39 |
117,15% |
6,67% |
1/3 |
-1,10 |
108,62% |
6,32% |
5/12 |
-0,88 |
102,01% |
6,03% |
1/2 |
-0,69 |
96,61% |
5,80% |
3/4 |
-0,29 |
84,59% |
5,24% |
1 |
0,00 |
76,07% |
4,83% |
1 3/4 |
0,56 |
59,49% |
3,97% |
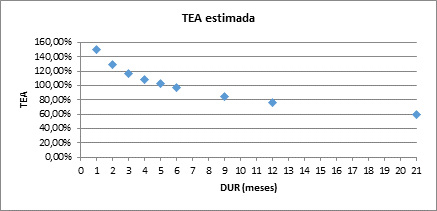
F uente. Elaboración propia en base a IAMC.
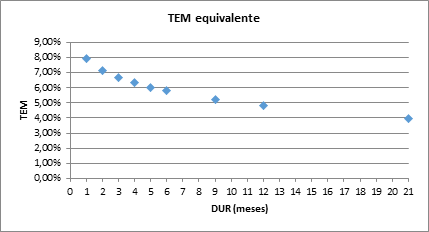
Fuente. Elaboración propia en base a IAMC.
La Tasa Efectiva Anual (TEA) estimada surge de aplicar la ecuación ( 26), mientras que la Tasa Efectiva Mensual (TEM) resulta de:
|
( 27) |
Para la construcción de la estructura temporal de volatilidades se utiliza como fuente las expectativas del mercado, en particular, las expectativas compiladas por el Banco Central de la República Argentina (BCRA) (2020) en el ejercicio mensual de Relevamiento de Expectativas de Mercado (REM).
Las expectativas que se han utilizado son el desvío reportado de la predicción de la tasa de interés BADLAR. Se considera que dicha información es relevante ya que los bonos pueden ser entendidos como un derivado sobre una tasa de interés. Dentro del universo de bonos seleccionados tenemos dos casos: (i) bonos a tasa variable BADLAR más spread para el caso del TB21 y (ii) bonos indexados por índice CER. Para con el primer grupo, la relación con el subyacente es directa, mientras que para con el segundo, la volatilidad de la tasa BADLAR se considera un buen proxy de la volatilidad del índice CER, teniendo en consideración la alta correlación entre ambas variables para el caso argentino (Basco, 2006).
Tasa de interés (BADLAR) |
|||||||||||
Período |
Referencia |
Mediana |
Promedio |
Desvío |
Máximo |
Mínimo |
Percentil 90 |
Percentil 75 |
Percentil 25 |
Percentil 10 |
Participantes |
30/4/2020 |
TNA; % |
27,71 |
28,30 |
2,97 |
38,00 |
25,00 |
31,40 |
28,80 |
26,40 |
26,00 |
34,00 |
31/5/2020 |
TNA; % |
27,11 |
27,66 |
3,24 |
38,00 |
22,70 |
30,70 |
28,70 |
25,63 |
24,45 |
34,00 |
30/6/2020 |
TNA; % |
27,05 |
27,37 |
3,20 |
38,00 |
21,01 |
29,84 |
28,78 |
25,62 |
24,30 |
34,00 |
31/7/2020 |
TNA; % |
26,90 |
27,28 |
3,33 |
36,00 |
21,01 |
30,93 |
28,88 |
25,03 |
23,54 |
34,00 |
31/8/2020 |
TNA; % |
27,05 |
27,12 |
3,53 |
36,30 |
21,01 |
31,40 |
28,54 |
25,00 |
23,30 |
34,00 |
30/9/2020 |
TNA; % |
26,60 |
27,32 |
4,97 |
48,65 |
21,01 |
31,40 |
28,08 |
24,78 |
23,00 |
34,00 |
próx. 12 meses |
TNA; %; mar-21 |
25,00 |
26,45 |
7,19 |
60,00 |
18,00 |
30,10 |
27,70 |
23,75 |
20,00 |
31,00 |
2020 |
TNA; %; dic-20 |
25,83 |
26,95 |
6,06 |
55,00 |
18,50 |
31,26 |
28,00 |
24,00 |
22,24 |
34,00 |
2021 |
TNA; %; dic-21 |
24,00 |
24,37 |
7,01 |
55,00 |
15,00 |
29,01 |
25,84 |
20,00 |
18,90 |
30,00 |
Recapitulando, hasta ahora los esfuerzos se han concentrado en: (i) construir una curva de rendimientos, primero usando la información del mercado y luego estimando un modelo que permita obtener valores de tasas para determinados puntos del tiempo, y (ii) construir una curva de volatilidades usando las expectativas del mercado. Con dicha información, se arma la matriz para la estimación del árbol, usando el modelo de BDT.
DUR (meses) |
TEM equivalente |
Desvío BADLAR REM |
1 |
7,92% |
2,97% |
2 |
7,15% |
3,24% |
3 |
6,67% |
3,20% |
4 |
6,32% |
3,33% |
5 |
6,03% |
3,53% |
6 |
5,80% |
4,97% |
9 |
5,24% |
6,06% |
12 |
4,83% |
7,19% |
21 |
3,97% |
7,01% |
Para un horizonte de 4 períodos, el árbol queda definido como se muestra a continuación.
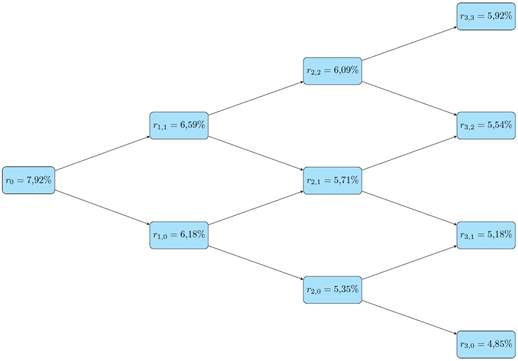
Fuente. Elaboración propia.
Utilizando la notación arriba definida, para i = 0, usamos la tasa resultante de la estimación de la curva de rendimientos, es decir:
|
( 28) |
Para i > 0, es necesario usar las ecuaciones del modelo para establecer los valores. Para el caso de i = 1:
|
(29) |
El valor de ![]() se obtiene a partir de ( 24), para este caso particular queda definido:
se obtiene a partir de ( 24), para este caso particular queda definido:
|
( 30) |
Reemplazando, la ecuación queda definida de la siguiente manera:
|
( 31) |
Una vez obtenido el valor para ![]() , se pueden obtener las tasas del resto de la rama usando las ecuaciones ya presentadas en ( 29).
, se pueden obtener las tasas del resto de la rama usando las ecuaciones ya presentadas en ( 29).
En particular,
|
( 32) |
El desarrollo para el resto de las ramas es similar y se detalla en el Apéndice II.
Las aplicaciones del árbol son múltiples, incluyendo la valuación de derivados sobre tasa de interés, por ejemplo, swaptions, bonos callables y notas estructuradas. Algunos ejemplos se pueden encontrar en Black, Derman y Toy (1990) y en Mina y Xiao (2001).
Conclusiones
A pesar de las conocidas complicaciones que presenta la economía argentina respecto de la falta de liquidez y de instrumentos que permitan armar curvas de rendimientos y volatilidades que puedan servir para el desarrollo de modelos, se comprueba que los escasos instrumentos e información utilizada alcanza para el caso descripto.
La estimación de la curva de rendimientos utilizando la metodología de IAMC (1998) pretende reflejar la manera en que los operadores del mercado lo hacen. La estimación no es la única posible y no se encuentra libre de inconvenientes. Un desarrollo extenso y actualizado de diferentes metodologías, con sus respectivas ventajas y desventajas, se encuentra en Rebonato (2018).
Se observa, tanto en la curva de rendimientos como en el árbol de tasas obtenido, que la pendiente de la curva de rendimientos es decreciente. Dicho resultado, si bien esperado contrasta con los resultados deseados por parte de diseñadores y reguladores, expresados, por ejemplo, en los 'Lineamientos de política monetaria' esgrimidos por el BCRA el día 27 de enero de 2020:
El nivel de tasa de interés real debe preservar la estabilidad financiera y externa de la economía, y debe ser compatible con el financiamiento de la producción y la construcción de una curva de rendimientos a mayor plazo, favoreciendo el ahorro en moneda doméstica. Esto último supone un manejo de tasas de interés donde se evitará que caiga en niveles reales negativos. (BCRA, 2020)
La razón de dicha falla no reside en un error de diseño de los instrumentos, ya que puede observarse que a mayor plazo el interés real que pagan los bonos sobre el índice de ajuste CER es mayor, sino en la manera que el mercado valúa los securities para acomodarlos a sus expectativas de tasas futuras. Más detalles de las implicancias y otras teorías relacionadas a curvas de rendimientos negativas pueden encontrarse en Más (2008).
Respecto de la implementación en un contexto de trading, es fundamental contar con la capacidad de cálculo que permita armar un árbol con saltos diarios y de recalibración a los precios de mercado en tiempo real.
Una línea de trabajo futuro que se puede proponer es calcular mensualmente el árbol, incluyendo una nueva curva de rendimientos y volatilidades para cada caso, con los objetivos de analizar la evolución del mercado, los efectos de las políticas de deuda implementadas y los ajustes resultantes de diferentes particularidades que estén operando en cada uno de los momentos (nivel de tasas, forma de la curva de rendimientos, cambios en los niveles de expectativas).
Además, se propone la realización de ejercicios de back-testing de cada una de las estimaciones contra lo realmente acontecido, ya que constituye la prueba más ácida del realismo de la estimación.
Apéndice I

Apéndice II
Para el resto de las ramas, el procedimiento es similar al descripto para el caso particular de i = 1.
Para el caso de i = 2:
|
(33) |
Además:
|
(34) |
El valor de ![]() se obtiene a partir de ( 24), para este caso particular queda definido:
se obtiene a partir de ( 24), para este caso particular queda definido:
|
( 35) |
Reemplazando, la ecuación queda definida de la siguiente manera:
|
( 36) |
Una vez obtenido el valor para ![]() , pueden obtenerse las tasas del resto de la rama usando las ecuaciones ya presentadas en ( 33) y ( 34).
, pueden obtenerse las tasas del resto de la rama usando las ecuaciones ya presentadas en ( 33) y ( 34).
Para el caso de i = 3:
|
(37) |
Además:
|
(38) |
Finalmente:
|
(39) |
El valor de ![]() se obtiene a partir de ( 24), para este caso particular queda definido:
se obtiene a partir de ( 24), para este caso particular queda definido:
|
( 40) |
Reemplazando, la ecuación queda definida de la siguiente manera:
|
( 41) |
Una vez obtenido el valor para ![]() , pueden obtenerse las tasas del resto de la rama usando las ecuaciones ya presentadas en ( 37), ( 38) y ( 39).
, pueden obtenerse las tasas del resto de la rama usando las ecuaciones ya presentadas en ( 37), ( 38) y ( 39).
[1] Los conceptos y opiniones vertidos en este trabajo son de exclusiva responsabilidad del autor.
[2] Agradezco el apoyo brindado por mi director de tesis doctoral, Javier García Fronti, de la cual este trabajo es parte y a la Facultad de Ciencias Económicas, Universidad de Buenos Aires, por permitirme realizar el doctorado.
- Basco, E. (2006). Crecimiento monetario e inflación: Argentina 1970-2005.
- BCRA. (2020). Resultados del Relevamiento de Expectativas de Mercado (REM). Descargado de https://www.bcra.gob.ar/PublicacionesEstadisticas/Relevamiento_Expectativas_de_Mercado.asp
- BCRA. (2020). [Lineamientos de política monetaria]. Descargado de:
- http://www.bcra.gov.ar/Noticias/BCRA-fijo-lineamientos-de-pol%C3%ADtica-monetaria270120.asp
- BOLSAR. (2020). [Descripción técnica de instrumentos]. Descargado
- dehttps://www.bolsar.com/VistasDL/PaginaPrincipal.aspx
- Black, F., Derman, E., & Toy, W. (1990). A One-Factor Model of Interest Rates and Its Application to Treasury Bond Options. Financial Analysts Journal, 46(1), 33-39.
- Brennan, Michael J., y Eduardo S. Schwartz. 1982. «An equilibrium model of bond pricing and a test of market efficiency». Journal of Financial and quantitative analysis 17(3):301-29.
- Heath, David, Robert Jarrow, y Andrew Morton. 1992. «Bond pricing and the term structure of interest rates: A new methodology for contingent claims valuation». Econometrica: Journal of the Econometric Society 77-105.
- Ho, T. S. Y., & Lee, S.-B. (1986). Term Structure Movements and Pricing Interest Rate Contingent Claims. The Journal of Finance, 41(5), 1011-1029.
- Hull, John, y Alan White. 1990. «Pricing Interest-Rate-Derivative Securities». The Review of Financial Studies 3(4):573-92.
- IAMC. (1998). Análisis de acciones. Descargado de https://www.iamc.com.ar/cuadernos/
- IAMC. (2020). [Flujos de fondos de bonos relevantes]. Descargado de
- https://www.iamc.com.ar/Financial/BondCalculator/
- IAMC. (2020). Informe diario. Descargado de https://www.iamc.com.ar/informediario/
- Lin, X. S., & Actuaries, S. of. (2006). Introductory Stochastic Analysis for Finance and Insurance. John Wiley & Sons.
- Longstaff, Francis A., y Eduardo S. Schwartz. 1992a. «A two-factor interest rate model and contingent claims valuation». The Journal of Fixed Income 2(3):16-23.
- Longstaff, Francis A., y Eduardo S. Schwartz. 1992b. «Interest rate volatility and the term structure: A two‐factor general equilibrium model». The Journal of Finance 47(4):1259-82.
- Más, A. (2008). Títulos Públicos y Obligaciones Negociables en el Mercado de Capitales Argentino. Ediciones Técnicas Empresariales SRL.
- Mina, J., & Xiao, J. Y. (2001). Return to RiskMetrics: The evolution of a standard. RiskMetrics Group, 1, 1-11.
- [Licitación para la conversión de instrumentos en el marco del decreto 1932020]. (2020). Descargado de https://www.argentina.gob.ar/noticias/llamado-licitacion-para-la-conversion-de-instrumentos-en-el-marco-del-decreto-1932020
- [Licitación para la conversión de Boncer 2020 - TC20 - en el marco del decreto 1932020]. (2020). Descargado de https://www.argentina.gob.ar/noticias/llamado-licitacion-para-la-conversion-de-boncer-2020-tc20-en-el-marco-del-decreto-1932020
- Rebonato, R. (1998). Interest-rate options models, Financial Engineering. Wiley.
- Rebonato, R. (2018). Bond Pricing and Yield Curve Modeling: A Structural Approach. Cambridge University Press.
BIBLIOGRAFÍA
Información del número
Revista de Investigación en Modelos Financieros
Volumen 2 - 2020
ISSN: 2250-687X
ISSN (En línea): 2250-6861