- Universidad Nacional de Córdoba, Facultad de Ciencias Económicas
- Universidad Nacional de Córdoba, Facultad de Ciencias Económicas
- Universidad Nacional de Córdoba, Facultad de Ciencias Económicas
RESUMEN
Palabras clave: Predicción; Rentabilidad; Random walk.
ABSTRACT
Keywords: Forecast; Profitability; Random walk.
INTRODUCCIÓN
Los modelos de valuación han identificado, claramente, que el valor de la empresa está vinculado a las expectativas de los resultados futuros (Ohlson, 1995), a la vez que los acreedores necesitan información sobre la rentabilidad para conocer la posibilidad de cobrar sus acreencias al momento de su vencimiento (Altman, 1968; Ohlson, 1980). A partir de la importancia de la predicción de los resultados se han desarrollado una variedad de modelos basados en la información de los estados financieros para predecir la rentabilidad, sin embargo, la investigación no ha avanzado lo suficiente. Desde la perspectiva del análisis fundamental, Arbanell y Bushee (1997) demuestran la utilidad de un conjunto de ratios que habitualmente son aplicados por los analistas financieros para la predicción de los resultados futuros. Otras investigaciones, ponen el acento en la persistencia de los componentes de los resultados, demostrando que la desagregación de los componentes (Richardson, Sloan, Soliman y Tuna, 2005; Esplin, Jewett, Plumlee y Yohn, 2014; Fairfield y Yohn, 2001) mejoran la precisión de los pronósticos. Terreno, Sattler y Castro Gonzalez (2018) para Argentina demuestran la capacidad predictiva de la desagregación en margen y rotación.
No obstante los estudios mencionados en el párrafo anterior, diversos autores señalan que la evidencia muestra que el pronóstico de la rentabilidad producido por varios modelos de regresión, no son más precisos que los generados por el proceso de random walk (Monahan, 2018; Fabris y da Costa, 2010). Gerakos y Gramacy (2013) demuestran que la complejidad de los modelos no agrega, en todos los casos, una mayor capacidad predictiva y que los métodos basados en MCO (Mínimos Cuadrados Ordinarios) y RW (random walk) desempeñan tan bien como los métodos más sofisticados de estimación. Monterrey Mayoral y Sánchez Segura (2017) sostienen que la calidad predictiva de los diferentes modelos es una cuestión de contexto que, además del método apropiado para cada caso depende del tipo de empresa analizada. En otro aspecto, si bien muchos estudios han mostrado mejoras estadísticamente significativas, éstas no resultan económicamente importantes (Vorst y Yohn, 2018; Farfield y Yohn, 2001).
En América Latina, la investigación sobre predicción de la rentabilidad ha sido insuficiente, la centralidad ha sido ocupada por la predicción de insolvencia. Las investigaciones han permitido cuestionar la utilidad de la información contable distinta de los resultados contables para la predicción. Para Swanson, Rees y Juárez-Valdés (2001) las señales fundamentales han demostrado ser un valor relevante en explicar los resultados futuros, solamente, posterior a la devaluación de México en diciembre 1994. Para empresas brasileñas que cotizan en el mercado de valores, De Albuquerque y Do Valle (2014) rechazan la hipótesis que el EVA® proporciona información adicional para el pronóstico de los resultados futuros. Fabris y Da Costa (2010) en un estudio de series de tiempo afirman que la rentabilidad operativa tiene un comportamiento aleatorio, descrito como RW con deriva.
Debido a las pobres evidencias de la capacidad predictiva de la información contable más allá de los resultados contables, este trabajo tiene por objetivo efectuar una evaluación de la capacidad predictiva de la rentabilidad de los modelos reversión a la media, de los ajustes de devengado y un conjunto de señales financieras comparados con relación al proceso de RW, en empresas del Mercado de Valores de Buenos Aires. En los estudios anteriores, la mayor parte de los estudios han sido llevados a cabo por el método de análisis de regresión por Mínimos Cuadrados Ordinarios (MCO), pero en este estudio se aplica el modelo de datos de panel con efectos fijos que incorpora al modelo la heterogeneidad no observada de las unidades (tecnología, capacidad de los administradores, cultura de la organización, etc.).
2. MARCO TEÓRICO
Los estudios sobre predicción de los resultados basadas en series temporales confirman que los resultados anuales de las empresas de Estados Unidos siguen un comportamiento aleatorio y que la predicción por modelos ARIMA no son más exactas que las procedentes de RW (Albretch, Lookabill y McKeon, 1977; Little, 1962). Estudios posteriores, demuestran la existencia de un proceso de reversión a la media en contra de la hipótesis de aleatoriedad (Fama y French, 2000; Baginski, Lorek, Willinger y Branson 1999; Lipe y Kormendi, 1994; Freeman, Ohlson y Penman, 1982). Los resultados por encima o debajo de la media desaparecen, revirtiendo a ésta por la presión competitiva del ambiente económico (Stigler, 1963). Para Fama y French (2000) la reversión a la media de la rentabilidad, medida por la rentabilidad de los activos, produce una variación predecible en los resultados. En esta etapa aparecen los estudios de datos longitudinales y el concepto de persistencia de los resultados. La propiedad de persistencia hace referencia a la permanencia de los resultados en el tiempo, contrario a los resultados transitorios, y representan un flujo constante para los inversores (Schipper y Vincent, 2003).
Los trabajos Ou (1990) y Arbanell y Bushee (1997) son los primeros en dar una evidencia de la vinculación entre la información financiera distinta a los resultados (nonearnings). Ou (1990) analiza una serie de ratios contables seleccionados estadísticamente. Los resultados indican que las cifras de las partidas financieras, distintas a resultados, contienen información sobre la dirección y no sobre la intensidad de los cambios en los resultados del próximo año. En cambio, Arbanell y Bushee (1997) utilizan las señales financieras fundamentales (variables contables identificadas por los inversores para pronosticar el grado de persistencia y crecimiento de los resultados). Los resultados del estudio Arbanell y Bushee (1997) indican que los inventarios, margen bruto, la tasa de impuestos, calidad de la información contable y fuerza laboral están significativamente relacionados con el cambio en los resultados futuros en el corto plazo; la tasa impositiva y la fuerza laboral permanecen en el largo plazo.
Otros estudios se enfocaron en la capacidad predictiva de los componentes de los resultados. Sloan (1996) sostiene que el grado en que los resultados actuales persisten en el futuro depende de la magnitud relativa de los flujos de efectivo y los ajustes por devengo. La empresa con altos (bajos) ajustes de devengado informados en el año contable tiende a tener bajos (altos) resultados futuros y rendimiento de las acciones. Para Farfield, Sweeney y Yohn (1996) la desagregación de los resultados (en resultados operativos, resultados no operacionales e impuestos, e ítems especiales) mejora la precisión de los pronósticos de la rentabilidad para el año siguiente, no así la separación de partidas extraordinarias y operaciones discontinuadas. Esplin, Jewett, Plumlee y Yohn (2014) encuentran que la desagregación del componente financiero tiene un muy pequeño efecto, mientras que la desagregación de los resultados de los activos operativos netos supera el modelo agregado. En relación con la clásica desagregación de Dupont, la evidencia muestra que el cambio en la rotación de activos es más perdurable que el cambio en el margen de ganancia, este último, tiene un efecto negativo o no significativo (Bauman, 2014; Penman y Zhang, 2002; Monterrey y Sánchez-Segura, 2011; Farfield y Yohn, 2001).
Recientes estudios, se han interesado en la aplicación de técnicas no paramétricas de clasificación para la predicción de la rentabilidad como redes neuronales y Machine Learning (Anand, Brunner, Ikegwu y Sougiannis, 2019; Mullainathan y Spiess, 2017; De Andrés, Landajo y Lorca, 2005).
2.1 Contexto de la economía argentina
Año |
%PBI (1) |
%IPC (2) (3) |
2006 |
8,00 |
9,80 |
2007 |
9,00 |
21,52 |
2008 |
4,10 |
20,60 |
2009 |
-5,90 |
18,47 |
2010 |
10,10 |
27,03 |
2011 |
6,00 |
23,28 |
2012 |
-1,00 |
23,01 |
2013 |
2,40 |
31,94 |
2014 |
-2,50 |
39,01 |
2015 |
2,70 |
31,57 |
2016 |
-2,10 |
40,90 |
1) Instituto Nacional de Estadística y Censos de la República Argentina;
(2) año 2006 y 2016: Instituto Nacional de Estadística y Censos de la República Argentina;
(3) año 2007-2015 Dirección de Estadística y Censos de San Luis.
En el período de estudio se puede identificar una primera etapa, desde el año 2006 al 2011, con un importante crecimiento económico, con excepción del año 2009 por la crisis económica mundial (Anuarios IAMC, 2006 a 2011). A partir del año 2008 aparece el déficit fiscal que se agrava a lo largo del tiempo y el superávit de cuenta corriente comienza a disminuir hasta ser negativo en 2010 por la disminución del tipo de cambio real. La segunda etapa desde el año 2012 al 2016 los desequilibrios económicos se agudizan por el decrecimiento del PBI, la aceleración de la tasa de inflación, el atraso cambiario y tarifario, el control de cambios y la falta de acceso a los mercados financieros internacionales (Anuarios IAMC, 2012 a 2015). A partir del 2016 la nueva administración nacional trató de volver rápidamente a una economía de mercado (Castiñeira, 2016). La Tabla N° 1 de los principales indicadores económicos (Producto Bruto Interno (PBI) e inflación de precios al consumidor (IPC)). Es evidente que los movimientos fluctuantes afectan la economía de las empresas, las variables económicas generan expectativas en todos los sectores y éstos adoptan posiciones defensivas u ofensivas de acuerdo con la evolución de la economía.
3. METODOLOGÍA
3.1 Modelos y variables
Para analizar la capacidad predictiva de la información financiera se plantean un conjunto de modelos.
a) Ramdon Walk (RW)
Los diferentes modelos de predicción son evaluados con relación a la hipótesis de paseo aleatorio (RW) como punto de referencia (benchmarking). El proceso de RW asume la aleatoriedad y, por lo tanto, el pronóstico menos erróneo es el comportamiento de la misma variable en el pasado reciente (Monterrey Mayoral y Sánchez Segura, 2017; Fairfield, Ramnath y Yohn, 2009). El supuesto básico de RW es el siguiente:
![]() (1)
(1)
Donde ![]() es una medida de la rentabilidad obtenida por la empresa i en el período t, y k es el número de períodos posteriores a t, esto aplicado a la rentabilidad del activo y a un año:
es una medida de la rentabilidad obtenida por la empresa i en el período t, y k es el número de períodos posteriores a t, esto aplicado a la rentabilidad del activo y a un año:
![]() (2)
(2)
donde:
![]()
![]()
![]()
b) Modelo reversión a la media (RM)
En una economía competitiva los beneficios por encima o por debajo de la media deberían desaparecer revirtiendo a la media (Fama y French, 2000; Mueller, 1977). El modelo de reversión es planteado de acuerdo con Farfield y Yohn (2001):
![]() (3)
(3)
donde
![]() (3.1)
(3.1)
De acuerdo con lo prescripto por la teoría es de esperar una relación negativa entre la ROA actual y la del año próximo (Penman y Zhang, 2002).
c) Modelo ajustes por devengo (AD)
El grado en que los resultados actuales persisten en el futuro depende de la magnitud relativa de los flujos de efectivo y los ajustes por devengo (De Albuquerque y Do Valle, 2014; Sloan, 1996). Además, son incluidas como variables de control las condiciones macroeconómicas (inflación y crecimiento de la economía). El modelo propuesto:
![]() (4)
(4)
Siendo:
![]()
![]()
![]()
![]()
![]()
La persistencia de ajustes por el devengado es menor que los flujos de efectivo, por lo cual se espera una relación negativa con los resultados futuros (Sloan, 1996). Cuando los estados financieros no son ajustados por inflación se produce una subestimación de los activos y pasivos, y una sobrestimación de los resultados con relación a los medidos en moneda constante. Pero, por otro lado, la inflación tiene un efecto negativo sobre el desempeño de las empresas y la economía. El crecimiento del PBI impacta de manera positiva sobre la mayor parte de las actividades.
d) Señales financieras de desempeño (DF)
Este modelo cubre un conjunto de variables de acuerdo con Piotroski (2000), aunque en el numerador de la ROA se utilizan los resultados antes de intereses e impuestos, en vez de los resultados netos, y el incremento de la rotación por la rotación del activo corriente y no corriente.
Rentabilidad: ![]()
Solvencia y liquidez: ![]()
Eficiencia operativa: ![]()
Contexto macroeconómico: ![]()
![]() (5)
(5)
Siendo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
El aumento de endeudamiento indica la incapacidad de la empresa para generar fondos internamente (Myers, 1984) y Chiou y Cheng (2006) indican que una mayor inversión en capital corriente reduce la rentabilidad, lo cual supone una relación negativa entre ∆LEVE y ∆LC con los cambios de la ROA del año próximo. El aumento del margen bruto se produce por un incremento del precio de venta o una disminución de los costos, esto implica un mayor potencial de generación de resultados. Una mayor rotación del activo corriente y no corriente indica una mayor eficiencia por el uso de los activos, si bien depende del sector de actividad y estrategias de la empresa (Wahlen, Baginski, y Bradsaw, 2011). Por lo mencionado, se espera una relación positiva entre ∆MB, RAC y RANC con el cambio de la ROA para el año próximo. Cuando se incrementa la inflación tiende a incrementarse el margen bruto por la falta de ajuste de los inventarios iniciales.
3.2 Datos
La población objeto de este estudio son todas las empresas no financieras autorizadas a cotizar en el Mercado de Valores de Buenos Aires en el período 2006 a 2016, excluidas las de capital extranjero. Las observaciones de la muestra están constituidas por datos de los estados financieros anuales consolidados, elaborados bajo Normas Contables Profesionales de la Federación Argentina de Consejos Profesionales de Ciencias Económicas (FACPCE) hasta el 31/12/2011 y por Normas Internacionales de Información Financiera (NIIF) a partir de ejercicios iniciados del año 01/01/2012. Los datos corresponden a una estructura de datos de panel no balanceado. La muestra inicial es de 574 observaciones y después de eliminar los datos atípicos (outliers) quedaron 527 observaciones de 72 empresas. Han sido considerados outliers aquellas observaciones que se alejan 3 veces la desviación estándar de la media. Las cifras de los estados financieros no se encuentran ajustados por inflación a pesar de la existencia de un contexto inflacionario, aunque no produce mayor distorsión en los resultados estadísticos.
|
Global |
|
Año |
Media |
Mediana |
2006 |
0,1130 |
0,0981 |
2007 |
0,1157 |
0,1104 |
2008 |
0,1033 |
0,1013 |
2009 |
0,1142 |
0,0992 |
2010 |
0,1211 |
0,1225 |
2011 |
0,1386 |
0,1306 |
2012 |
0,1001 |
0,0907 |
2013 |
0,1071 |
0,0967 |
2014 |
0,1368 |
0,1528 |
2015 |
0,1655 |
0,1544 |
2016 |
0,1604 |
0,1781 |
Total |
0,1251 |
0,1183 |
La Tabla N° 2 muestra la evolución de la rentabilidad por año. Los mayores niveles de ROA corresponden a los años 2010, 2011, 2014 y 2016, los dos primeros corresponden con un período de crecimiento de la economía y los últimos a la alta inflación.
Variables |
Media |
Mediana |
Desv. Est. |
0,0349 |
0,0025 |
0,0753 |
|
ROAt |
0,1214 |
0,1132 |
0,1037 |
∆ROAt |
0,0172 |
0,0082 |
0,0921 |
DEBEt |
(0,2646) |
(0,2031) |
0,2292 |
∆IPCt |
18,1907 |
19,3100 |
6,3669 |
∆PBIt |
2,4975 |
2,7312 |
5,0187 |
∆LEVEt |
(0,1218) |
(0,0047) |
0,1276 |
∆LCt |
(0,0513) |
(0,0200) |
0,5057 |
∆MBt |
0,0321 |
0,0053 |
0,1383 |
RACt |
2,4598 |
2,2446 |
1,1773 |
RANCt |
0,5182 |
0,4886 |
0,2856 |
|
ROAt+1 |
ROAt |
∆ROAt |
DEVEt |
∆IPCt |
∆PBIt |
ROAt+1 |
1,000 |
|||||
ROAt |
(0,336) |
1,000 |
||||
∆ROAt |
(0,331) |
0,415 |
1,000 |
|||
DEVEt |
(0,097) |
(0,290) |
(0,021) |
1,000 |
||
∆IPCt |
0,044 |
(0,071) |
(0,207) |
(0,052) |
1,000 |
|
∆PBIt |
0,035 |
(0,040) |
0,165 |
0,059 |
0,232 |
1,000 |
∆LEVEt |
(0,036) |
0,026 |
(0,027) |
(0,039) |
0,146 |
(0,082) |
∆LCt |
(0,117) |
0,131 |
0,161 |
(0,010) |
0,014 |
0,073 |
∆MBt |
(0,059) |
0,090 |
0,450 |
(0,010) |
(0,241) |
0,312 |
RACt |
(0,030) |
(0,067) |
(0,032) |
(0,334) |
0,079 |
0,015 |
RANCt |
0,091 |
0,306 |
0,044 |
(0,389) |
(0,030) |
(0,042) |
|
∆LEVEt |
∆LCt |
∆MBt |
RACt |
RANCt |
|
ROAt+1 |
||||||
ROAt |
||||||
∆ROAt |
||||||
DEVEt |
||||||
∆IPCt |
||||||
∆PBIt |
||||||
∆LEVEt |
1,000 |
|||||
∆LCt |
0,264 |
1,000 |
||||
∆MBt |
(0,144) |
0,105 |
1,000 |
|||
RACt |
(0,053) |
0,004 |
(0,011) |
1,000 |
||
RANCt |
(0,010) |
(0,040) |
(0,059) |
(0,299) |
1,000 |
La Tabla N° 3 muestra los estadísticos descriptivos del conjunto de variables utilizadas. Las variables definidas como incrementos muestran una mayor diferencia entre la media y mediana, indicando una distribución asimétrica de los datos. El ∆PBI muestra la mayor dispersión, lo cual confirma un contexto de inestabilidad. La Tabla N° 4 muestra los coeficientes de correlación, en general la correlación entre variables es baja por lo cual no se presentaría problema de colinealidad.
3.3 Modelo de efectos fijos
Los modelos de regresión son estimados por el modelo de datos de panel con efecto fijos. Esta metodología posibilita capturar la heterogeneidad no observable entre las unidades o sea los efectos atribuibles específicamente a la empresa (Verbeek, 2000). De acuerdo con Balgati (1995) el modelo se puede plantear como:
![]() (6)
(6)
Si se descompone del término error:
![]() (7)
(7)
![]() representa los efectos no observables atribuibles específicamente a la empresa;
representa los efectos no observables atribuibles específicamente a la empresa;
![]() identifica los efectos no cuantificados que varían con el tiempo, pero no entre empresas;
identifica los efectos no cuantificados que varían con el tiempo, pero no entre empresas;
![]() se refiere al término error puramente aleatorio.
se refiere al término error puramente aleatorio.
Si se supone ![]() , o sea que no existen efectos no cuantificables que varíen en el tiempo se tiene que:
, o sea que no existen efectos no cuantificables que varíen en el tiempo se tiene que:
![]() (8)
(8)
Es decir, que el error puede descomponerse en dos, una parte fija definida con una constante para cada individuo ![]() y otra aleatoria que cumplen con los requisitos MCO
y otra aleatoria que cumplen con los requisitos MCO![]() , lo que equivalente a obtener una tendencia general por regresión y un punto de origen (ordenada) por individuo.
, lo que equivalente a obtener una tendencia general por regresión y un punto de origen (ordenada) por individuo.
|
Modelo RM |
Modelo AD |
Modelo FD |
||||
Test |
Coef. |
p-value |
Coef. |
p-value |
Coef. |
p-value |
|
Test de Hausman |
90,240 |
0,00 |
108,230 |
0,00 |
143,780 |
0,00 |
|
Test F de restricciones |
2,100 |
0,00 |
2,370 |
0,00 |
2,740 |
0,00 |
|
Test para heterocedasticidad |
9.939 |
0,00 |
4.495 |
0,00 |
2.617 |
0,00 |
|
Test para correlación contemporánea |
4,239 |
0,00 |
0,307 |
0,76 |
0,013 |
0,99 |
|
Test para correlación serial |
48,028 |
0,00 |
45,608 |
0,00 |
40,049 |
0,00 |
|
Test F restricción temporal |
3,050 |
0,00 |
2,070 |
0,05 |
2,150 |
0,04 |
|
Skewness/Kurtosis test de normalidad |
11,92 |
0,00 |
15,96 |
0,00 |
15,65 |
0,00 |
|
La Tabla N° 5 presenta el test de especificaciones del modelo de datos de panel. Primero, se debe determinar si es más conveniente el modelo de efectos fijos o el modelo de efectos aleatorios. Para los efectos fijos existe un término constante para cada individuo, independientes entre sí, en los efectos aleatorios los efectos individuales no son independientes entre sí y están distribuidos aleatoriamente alrededor de un valor dado. Los efectos aleatorios son más eficientes cuando el modelo es verdadero, pero es inconsistente cuando el modelo está mal especificado. Los efectos fijos son consistentes cuando el modelo está mal especificado, pero no es eficiente cuando el modelo es verdadero (Verbeek, 2000). El test de Hausman rechaza la hipótesis nula de igualdad de los residuos, la diferencia entre los coeficientes es significativa, en consecuencia, el modelo de efectos fijos es preferido al aleatorio ya que es consistente, aunque pierda eficiencia. Por otra parte, el test de F de restricción rechaza la hipótesis nula de igualdad de residuos, indicando la presencia de efectos individuales, por lo tanto, el modelo de efecto fijos es superior al MCO. El test F de restricción temporal (to-way fixed effects) rechaza la hipótesis nula, por lo que es posible afirmar que las variables dicotómicas temporales, una para cada año, son en conjunto significativas. No obstante, no son incluidas en el modelo debido a que no modifican de forma importante los resultados de los modelos.
Una segunda cuestión para tener presente es que el modelo de efectos fijos puede presentar algunos problemas. La varianza de los errores de cada unidad transversal puede no ser constante (heteroscedasticidad) violando el supuesto de varianza constante. Los errores entre unidades pueden estar correlacionados al mismo tiempo (correlación contemporánea) o dentro de cada unidad pueden estar correlacionados temporalmente (correlación serial), violando el supuesto de independencia de los errores. Esto, si bien no afecta la consistencia de los estimadores, sí impacta en la eficiencia. El test Wald para heteroscedasticidad rechaza la hipótesis nula de homocedasticidad en todos los modelos. El test de Pesaran (2004) acepta la hipótesis de no correlación contemporánea para los modelos AD y DF. El test de Woldridge rechaza la hipótesis nula de no presencia de correlación serial de primer orden para los tres modelos. Para resolver la violación de los supuestos del modelo de efectos fijos, la estimación de los parámetros se efectuó mediante efectos fijos individuales con corrección de errores de Driscoll y Kraay (1998) (Hoechle, 2007). Este método produce un estimador no paramétrico con errores estándar consistentes frente a la heterocesdasticidad y robustos a formas muy generales de dependencia espacial y temporal, y es aplicable para el caso de N>T inclusive con panel de datos no balanceado (Driscoll y Kraay, 1998). El test Shapiro-Wilks rechaza la hipótesis de normalidad de los residuos, aunque la Figura N° 1 muestra una distribución de datos aproximada a la normal
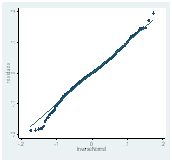
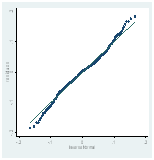
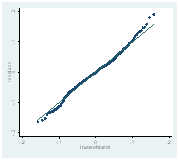
Modelo RM Modelo AD Modelo FD
La tercera cuestión, es medir la precisión de los pronósticos con efectos fijos y MCO y las métricas utilizadas son:
a) Error Absoluto Medio:
![]() (9)
(9)
b) Mediana Error Absoluto:
![]() (10)
(10)
n: tamaño de la muestra;
![]() : es la estimación de
: es la estimación de ![]() .
.
La media es un estadístico sensible a los valores extremos cuando la distribución no es simétrica, mientras que la mediana no es alterada por los extremos. El test para analizar la significatividad de las diferencias de las medias utilizado es el estadístico t-student y la diferencia de las medianas por el test de rangos de Wilcoxon.
Modelo RM |
Modelo AD |
Modelo DF |
|
Error absoluto medio |
|||
Modelo de efectos fijos |
0,04559 |
0,04349 |
0,04148 |
Modelo MCO |
0,05242 |
0,05088 |
0,05000 |
Mejora modelo efectos fijos |
0,00683 |
0,00739 |
0,00852 |
estadístico t |
5,688 |
5,922 |
6,528 |
p-value |
0,000 |
0,000 |
0,000 |
|
Modelo RM |
Modelo AD |
Modelo FD |
Mediana error absoluto |
|||
Modelo de efectos fijos |
0,03534 |
0,033425 |
0,03059 |
Modelo MCO |
0,04077 |
0,04073 |
0,03892 |
Mejora modelo efectos fijos |
0,00543 |
0,007305 |
0,00833 |
Test de rangos de Wilcoxon |
5,630 |
5,670 |
6,039 |
p-value |
0,000 |
0,000 |
0,000 |
Los errores en valores absolutos son determinados con los datos in-sample y son medidos por la media (MAE) y la mediana (MdAE) en tanto por 1.
La Tabla N° 6 demuestra que los pronósticos por el modelo de efectos fijos tienen una mayor precisión que los pronósticos por MCO, cuyos coeficientes son iguales al modelo de datos de panel con efectos aleatorios, las mejoras en la rentabildiad alcanzan valores entre 0,54% y 0,83% y son estadísticamente significativos.
3.4 Resultados
Modelo RM |
Modelo AD |
Modelo DF |
|
Error absoluto medio |
|||
Modelo de efectos fijos |
0,04559 |
0,04349 |
0,04148 |
Modelo MCO |
0,05242 |
0,05088 |
0,05000 |
Mejora modelo efectos fijos |
0,00683 |
0,00739 |
0,00852 |
estadístico t |
5,688 |
5,922 |
6,528 |
p-value |
0,000 |
0,000 |
0,000 |
|
Modelo RM |
Modelo AD |
Modelo FD |
Mediana error absoluto |
|||
Modelo de efectos fijos |
0,03534 |
0,033425 |
0,03059 |
Modelo MCO |
0,04077 |
0,04073 |
0,03892 |
Mejora modelo efectos fijos |
0,00543 |
0,007305 |
0,00833 |
Test de rangos de Wilcoxon |
5,630 |
5,670 |
6,039 |
p-value |
0,000 |
0,000 |
0,000 |
La estimación es efectuada por el método de datos de panel con efectos fijos. R2 : coeficiente de determinación
La Tabla N° 7 muestra los resultados obtenidos de la estimación de modelos. El coeficiente de la rentabilidad del activo (ROAt) es significativo para los 3 modelos y exhiben una relación negativa con la rentabilidad futura, lo cual confirma la reversión a la media de la rentabilidad. El modelo DF muestra un coeficiente superior a los otros modelos (![]() =-0,59545), lo cual indica una mayor permanecia de la rentabilidad. El ∆ROAt también muestra un coeficiente negativo, pero es significativo en los 3 modelos para un nivel de significación de 0,10. Los ajustes de devengado (DEVEt) son significativos y negativos para los 2 modelos, los mayores ajustes implican una menor ROA en el próximo ejercicio. El coeficiente de la tasa de inflación (∆IPC) es negativa y el crecimiento de la economía (∆PBI) positiva, siendo ambas significativas para el modelo AD, aunque para el modelo FD solamente es significativo el ∆PBI. El signo negativo de la tasa de la inflación se debe a que afecta de manera desfavorable el desempeño futuro de la empresa. El resto de las variables del modelo FD, solamente el cambio en la LC y la RANC muestran un efecto significativo, el primero negativo y el segundo positivo. El mayor valor del R2 (coeficiente de determinación) corresponde al modelo FD (R2 =42,89), en segundo lugar, el modelo AD (R2 =36,72), y por último el modelo RM (R2 =30,78), lo cual nos sirve para analizar la importancia de las variables. Los R2 parciales, no tabulados, confirman la importancia de la ROA actual en la explicación del ROA futuro, en segundo lugar, los ajustes por devengo y la rotación de los activos no corrientes, o sea el R2 del modelo FD se explica, esencialmente, por la inclusión de estas 3 variables.
=-0,59545), lo cual indica una mayor permanecia de la rentabilidad. El ∆ROAt también muestra un coeficiente negativo, pero es significativo en los 3 modelos para un nivel de significación de 0,10. Los ajustes de devengado (DEVEt) son significativos y negativos para los 2 modelos, los mayores ajustes implican una menor ROA en el próximo ejercicio. El coeficiente de la tasa de inflación (∆IPC) es negativa y el crecimiento de la economía (∆PBI) positiva, siendo ambas significativas para el modelo AD, aunque para el modelo FD solamente es significativo el ∆PBI. El signo negativo de la tasa de la inflación se debe a que afecta de manera desfavorable el desempeño futuro de la empresa. El resto de las variables del modelo FD, solamente el cambio en la LC y la RANC muestran un efecto significativo, el primero negativo y el segundo positivo. El mayor valor del R2 (coeficiente de determinación) corresponde al modelo FD (R2 =42,89), en segundo lugar, el modelo AD (R2 =36,72), y por último el modelo RM (R2 =30,78), lo cual nos sirve para analizar la importancia de las variables. Los R2 parciales, no tabulados, confirman la importancia de la ROA actual en la explicación del ROA futuro, en segundo lugar, los ajustes por devengo y la rotación de los activos no corrientes, o sea el R2 del modelo FD se explica, esencialmente, por la inclusión de estas 3 variables.
3.5 Validación de los modelos
La validación de los modelos predictivos significa comprobar si el modelo predice bien la variable dependiente. El análisis del poder explicativo de las variables por el coeficiente de determinación no resulta útil para determinar la capacidad predictiva. De entre las técnicas de validación más conocidas se aplicará el método de validación aparente (apparent validation), por este método se utiliza la misma muestra que para el cálculo de los coeficientes modelo (in-sample). Este método es útil como un indicador potencial de la capacidad predictiva. En segundo lugar, como técnica de validación se aplicará la división de los datos que consiste en dividir la muestra original en dos submuestras, una en que se calculan los coeficientes del modelo (training) y la otra con los datos fuera de la muestra (out-of-sample) se valida el modelo (test). La precisión de los pronósticos es medida por el Error Absoluto Medio y la Mediana Error Absoluto.
Modelo RM |
Modelo AD |
Modelo DF |
|
Error absoluto medio |
|||
Modelo de efectos fijos |
0,04559 |
0,04349 |
0,04148 |
Modelo MCO |
0,05242 |
0,05088 |
0,05000 |
Mejora modelo efectos fijos |
0,00683 |
0,00739 |
0,00852 |
estadístico t |
5,688 |
5,922 |
6,528 |
p-value |
0,000 |
0,000 |
0,000 |
|
Modelo RM |
Modelo AD |
Modelo FD |
Mediana error absoluto |
|||
Modelo de efectos fijos |
0,03534 |
0,033425 |
0,03059 |
Modelo MCO |
0,04077 |
0,04073 |
0,03892 |
Mejora modelo efectos fijos |
0,00543 |
0,007305 |
0,00833 |
Test de rangos de Wilcoxon |
5,630 |
5,670 |
6,039 |
p-value |
0,000 |
0,000 |
0,000 |
Los errores en valores absolutos son determinados con los datos in-sample y son medidos por la media (MAE) y la mediana (MdAE) en tanto por 1.
La Tabla N° 8 muestra un menor error en los pronósticos de los modelos en relación con RW, la menor diferencia corresponde a la media del modelo FD es de 1,35% y para la mediana la diferencia es de 0,64%. Analizado por empresa, la mayor precisión indica que los 3 modelos son superiores a RW y entre los modelos es superior FD.
|
Random Walk |
Modelo RM |
Modelo AD |
Modelo FD |
|||||
|
n |
Media |
Mediana |
Media |
Mediana |
Media |
Mediana |
Media |
Mediana |
Decil 1 |
53 |
-0,14291 |
-0,13145 |
-0,11200 |
-0,10408 |
-0,10600 |
-0,10196 |
-0,09925 |
0,09894 |
Decil 2 |
53 |
-0,07040 |
-0,07025 |
-0,05717 |
-0,05809 |
-0,05335 |
-0,05369 |
-0,05181 |
-0,05103 |
Decil 3 |
53 |
-0,04386 |
-0,04400 |
-0,03453 |
-0,03280 |
-0,03439 |
-0,03510 |
-0,03226 |
-0,03108 |
Decil 4 |
53 |
-0,25261 |
-0,02620 |
-0,01874 |
-0,01713 |
-0,01963 |
-0,01959 |
-0,01792 |
-0,01801 |
Decil 5 |
53 |
-0,00888 |
-0,00840 |
-0,00519 |
-0,00360 |
-0,00337 |
-0,00277 |
-0,00590 |
-0,00578 |
Decil 6 |
53 |
0,00482 |
0,00520 |
0,00698 |
0,00735 |
0,00845 |
0,00844 |
0,00705 |
0,00646 |
Decil 7 |
53 |
0,01790 |
0,01770 |
0,02070 |
0,02063 |
0,01997 |
0,20217 |
0,01881 |
0,01840 |
Decil 8 |
52 |
0,03383 |
0,03300 |
0,03720 |
0,03641 |
0,03235 |
0,03213 |
0,03140 |
0,03008 |
Decil 9 |
52 |
0,06247 |
0,06180 |
0,05930 |
0,05800 |
0,05400 |
0,05443 |
0,05262 |
0,05291 |
Decil 10 |
52 |
0,14107 |
0,13750 |
0,10625 |
0,09743 |
0,10458 |
0,09726 |
0,09982 |
0,09101 |
La Tabla N° 9 muestra los errores de predicción agrupados en deciles que nos permite conocer la distribución de éstos y, por lo tanto, el riego de la estimación. Los errores en los deciles superior e inferior son bastantes importantes y representan un 20% de la muestra y, en general, son el doble del valor del decil siguiente.
Modelo RM vs RW |
Modelo AD vs RW |
Modelo FD vs RW |
|||||||
Mejora |
t/w |
p-value |
Mejora |
t/w |
p-value |
Mejora |
t/w |
p-value |
|
MAE |
0,00936 |
5,7828 |
0,00 |
0,01107 |
6,722 |
0,00 |
0,01347 |
7,4045 |
0,00 |
MdAE |
0,00261 |
5,0430 |
0,00 |
0,00438 |
5,922 |
0,00 |
0,00721 |
6,4860 |
0,00 |
Modelo AD vs Modelo RM |
Modelo FD vs Modelo RM |
Modelo FD vs Modelo AD |
|||||||
Mejora |
t/w |
p-value |
Mejora |
t/w |
p-value |
Mejora |
t/w |
p-value |
|
MAE |
0,00171 |
3,1344 |
0,00 |
0,00411 |
4,3352 |
0,00 |
0,00240 |
2,7690 |
0,00 |
MdAE |
0,00177 |
2,7800 |
0,01 |
0,00460 |
4,0560 |
0,00 |
0,00283 |
2,5420 |
0,01 |
Las mejoras surgen de las diferencias de errores absolutos y un menor error es planteado de forma positiva con los datos in-sample y son medidos por la media (MAE) y la mediana (MdAE), en tanto por 1. El test para analizar la significatividad de las medias utilizado es el estadístico t y las medianas por el test de rangos de Wilcoxon.
La Tabla N° 10 muestra los resultados del test de validación con datos in-sample demuestra que todos los modelos analizados son superiores a RW y las mejoras significativas, tanto de la media y mediana. La mejora en la rentabilidad para el modelo RM es de 0,94%, modelo AD es de 1,11% y el modelo FD de 1,35%, si bien la mediana muestra una mejora bastante inferior para el modelo RM de 0,26%, modelo AD es de 0,44% y el modelo FD es de 0,72%, lo cual se debe a que no se contemplan los valores extremos. A su vez, la mejora del modelo de FD es superior y significativa a los modelos de RM y AD, la media de las mejoras son 0,41%, y 0,24% respectivamente; a la vez el modelo AD muestra una mejora significativa con relación a RM, pero no es económicamente importante.
|
RW |
Modelo RM |
Modelo AD |
Modelo FD |
MAE |
0,06871 |
0,06761 |
0,06282 |
0,05885 |
MdAE |
0,05200 |
0,05070 |
0,04612 |
0,04932 |
Pérdidas de precisión (con relación a RW) |
|
|
|
|
MAE |
12,55% |
10,13% |
9,50% |
|
MdAE |
3,27% |
0,21% |
10,67% |
|
Mejor método por empresa |
|
|
|
|
cantidad |
17 |
8 |
11 |
19 |
Los coeficientes son determinados con las observaciones de los 7 años anterior al año del pronóstico. Los errores en valores absolutos son medidos por la media (MAE) y la mediana (MdAE), en tanto por 1.
La Tabla N° 11 informa de los errores de predicción de los pronósticos con datos out-of-sample, la media del menor error de predicción de la rentabilidad corresponde al modelo FD de un 5,89% y el mayor error corresponde a RW con 6,87%. Por la mediana el menor error corresponde al modelo AD con 4,61% y el mayor error corresponde a RW con 5,20%. En cuanto al modelo que mejor ajusta por empresa, el modelo FD en 19 empresas y RW 17 en empresas, mientras que los otros 2 modelos una cantidad bastante inferior, esto indica que no hay un método que sea superior para todas las empresas.
Modelo RM vs RW |
Modelo AD vs RW |
Modelo FD vs RW |
|||||||
Mejoría |
t/w |
p-value |
Mejoría |
t/w |
p-value |
Mejoría |
t/w |
p-value |
|
MAE |
0,00110 |
0,2721 |
0,39 |
0,00588 |
1,4674 |
0,07 |
0,00985 |
2,6405 |
0,00 |
MdAE |
0,00130 |
0,2030 |
0,84 |
0,00588 |
1,3740 |
0,17 |
0,00268 |
2,3490 |
0,02 |
Modelo AD vs Modelo RM |
Modelo FD vs Modelo RM |
Modelo FD vs Modelo AD |
|||||||
Mejoría |
t/w |
p-value |
Mejoría |
t/w |
p-value |
Mejoría |
t/w |
p-value |
|
MAE |
0,0048 |
2,2370 |
0,01 |
0,0088 |
3,4618 |
0,00 |
0,0040 |
2,4481 |
0,01 |
MdAE |
0,0046 |
2,1580 |
0,03 |
0,0014 |
3,0910 |
0,00 |
(0,0032) |
2,2080 |
0,03 |
Modelo RM vs RW |
Modelo AD vs RW |
Modelo FD vs RW |
|||||||
Mejoría |
t/w |
p-value |
Mejoría |
t/w |
p-value |
Mejoría |
t/w |
p-value |
|
año: 2014 |
|||||||||
MAE |
0,00301 |
0,5580 |
0,28 |
0,00672 |
1,2651 |
0,11 |
0,00583 |
1,0350 |
0,15 |
MdAE |
0,01117 |
0,7840 |
0,43 |
0,01253 |
1,5410 |
0,12 |
0,00874 |
1,3260 |
0,18 |
año: 2015 |
|||||||||
MAE |
-0,00092 |
-0,1431 |
0,44 |
0,00340 |
0,5097 |
0,31 |
0,00709 |
1,1473 |
0,13 |
MdAE |
-0,00360 |
-0,3980 |
0,72 |
-0,00043 |
0,3560 |
0,72 |
-0,00859 |
0,954 |
0,34 |
año: 2016 |
|||||||||
MAE |
0,00053 |
0,0618 |
0,48 |
0,00323 |
0,3928 |
0,35 |
0,01445 |
1,9619 |
0,03 |
MdAE |
-0,00064 |
0,3070 |
0,76 |
0,00117 |
1,3650 |
0,17 |
0,01303 |
2,444 |
0,01 |
Los coeficientes son determinados con las observaciones de los 7 años anteriores al año del pronóstico. Los errores en valores absolutos son medidos por la media (MAE) y la mediana (MdAE), en tanto por 1. El test para analizar la significatividad de las medias utilizado es el estadístico t y las medianas el test de rangos de Wilcoxon.
La Tabla N° 12 informa las mejoras en la precisión de los pronósticos con datos out-of-sample. Globalmente, el modelo FD muestra mejoras significativas respecto a RW para la media de la rentabilidad de 0,99% y para la mediana de 0,27%. Las mejoras de los modelos RM y AD en relación con RW son positivas, pero no significativas. A la vez que el modelo FD evidencia una mejora positiva y significativa respecto al modelo AD y RM. Las mejoras de la rentabilidad medida por la media son de 0,88% y 0,40% y la mediana es de 0,14% y -0,32%, respectivamente. Si bien la última medición muestra ser negativa, de acuerdo con los signos del test de Wilcoxon es positiva[1].
|
Modelo FD |
||
|
n |
Media |
Mediana |
Decil 1 |
14 |
0,00438 |
0,00450 |
Decil 2 |
14 |
0,01219 |
0,01117 |
Decil 3 |
14 |
0,02419 |
0,02414 |
Decil 4 |
14 |
0,03448 |
0,03441 |
Decil 5 |
14 |
0,04452 |
0,04351 |
Decil 6 |
14 |
0,06000 |
0,05626 |
Decil 7 |
14 |
0,06769 |
0,06747 |
Decil 8 |
13 |
0,08190 |
0,07875 |
Decil 9 |
13 |
0,10711 |
0,10716 |
Decil 10 |
13 |
0,17415 |
0,17262 |
En el análisis de la predicción por cada año, los modelos AD y FD muestran una mejora con relación a RW en casi todos los años, pero solamente resulta significativo el modelo FD para el año 2016, con una mejora de la rentabilidad para la media y mediana del 1,45%. y 1,30%, respectivamente. La Tabla N° 13 muestra la distribución de los errores, los tres deciles inferiores señalan que los errores superiores al 6,769% representan un 30% del total.
CONCLUSIONES
El estudio se plantea evaluar la capacidad predictiva de la rentabilidad de los modelos de reversión a la media, ajustes por devengo y señales financieras de desempeño con relación al proceso de random walk de las empresas del Mercado de Valores de Buenos Aires. La economía argentina tiene la particularidad de desenvolverse en un contexto turbulento, con desajustes macroeconómicos y sujeta a crisis recurrentes y prolongadas. El estudio de la rentabilidad es efectuado por la rentabilidad de activo. La primera conclusión es de tipo metodológica, el método de datos de panel con efectos fijos exhibe una mayor precisión de los pronósticos de la rentabilidad en relación con MCO, la mejora en la rentabilidad medida por la media es entre 0,68% a 0,85%.
Segundo, el análisis de los modelos revela que la rentabilidad del activo actual es la principal variable que explica el cambio de la rentabilidad de los activos del año siguiente, ratificando lo sostenido por la mayor parte de la bibliografía. La relación entre ambas rentabilidades es negativa, confirmando la reversión a la media. Adicionalmente, existe un importante poder explicativo de los ajustes de devengado y la rotación de los activos no corrientes, siendo la relación negativa y positiva, respectivamente.
Tercero, la validación demuestra una mayor precisión de los pronósticos de los 3 modelos con relación a random walk y el modelomás preciso es el de las señales de desempeño financiero. Pero con datos out-of-sample, solamente,el modelo de señales financieras de desempeño muestra una mejora significativa. En la validación por año y empresa con datos out-of-sample las mejoras no son tan contundentes, el modelo de señales financieras de desempeño muestra una mejora significativa con relación a random walk solamente en un año de los tres. En cuanto al método más preciso por empresa, las diferencias entre el modelo de señales financieras de desempeño y random walk no son importantes. Esto último indicaría que la precisión en la predicción depende del contexto económico y de las características de la empresa. En consecuencia, random walk no debe descartárselo, en particular, cuando hay permanencia de la rentabilidad.
El estudio es un aporte a la investigación empírica en Latinoamérica y es de utilidad para inversores y acreedores. Un desafío para futuras investigaciones sería establecer el método de predicción más adecuado de acuerdo con el contexto y la empresa.
[1] Los conceptos y opiniones vertidos en este trabajo son de exclusiva responsabilidad del autor.
[2] Agradezco el apoyo brindado por mi director de tesis doctoral, Javier García Fronti, de la cual este trabajo es parte y a la Facultad de Ciencias Económicas, Universidad de Buenos Aires, por permitirme realizar el doctorado.
- Albretch, W.S., Lookabill, L. y McKeon, J. (1977). The time series properties of annual earnings. Journal of Accounting Research, 15, pp. 226-244.
- Anand, V., Brunner, R., Ikegwu, K. y Sougiannis, T. (2019). Predicting Profitability Using Machine Learning. Disponible en SSRN: https://ssrn.com/abstract=3466478
- Anuarios del Instituto Argentino del Mercado de Capitales-IAMC (2006-2015). Disponible en http: //www.iamc.sba.com.ar/informes/informe_anuario/
- Altman, E. (1968). Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. Journal of Finance 23, 589–609.
- Arbanell, J.S. y Bushee, B. J. (1997). Fundamental analysis, future earnings, and stock prices. Journal of Accounting Research, pp. 35, 1-24.
- Baginski, S. P.; Lorek, K. S.; Willinger, G. L. y Branson, B. C. (1999). The relationship between economic characteristics and alternative annual earnings persistence measures. The Accounting Review, 74(1), 105-120.
- Baltagi, B H. (1995). Econometric analysis of panel data (Vol. 2). New York: Wiley.
- Bauman, M. P. (2014). Forecasting operating profitability with DuPont analysis: Further evidence. Review of Accounting and Finance, 13(2), pp. 191-205.
- Castiñeira, R. (2016). El retorno de Argentina a una economía de mercado. Escenario 2017-2021. Econométrica: Informe Macro - diciembre 2016. Obtenido de https://www.econometrica.com.ar/ attachments/article/312/Econométrca%20-%20Informe% 20Macro%20-%20Dic-16.pdf
- Chiou, J. R., Cheng, L., & Wu, H. W. (2006). The determinants of working capital management. Journal of American Academy of Business, 10(1), pp. 149-155.
- De Albuquerque, A. A. y Do Valle, M. R. (2014). Capacity of Future Earnings´ Prediction of EVA® in the Brazilian Public Companies. International Business Research 8, 38-49.
- De Andrés, J., Landajo, M. y Lorca, P. (2005). Forecasting business profitability by using classification techniques: A comparative analysis based on a Spanish case. European Journal of Operational Research, 167(2), pp. 518-542.
- Driscoll, J. C., & Kraay, A. C. (1998). Consistent covariance matrix estimation with spatially dependent panel data. Review of economics and statistics, 80(4), pp. 549-560.
- Esplin, A., Hewitt, M., Plumlee, M. y Yohn, T. L. (2014). Disaggregating operating and financial activities: Implications for forecasts of profitability. Review of Accounting Studies 19, pp. 328-362.
- Fairfield, P. M., Sweeney, R. J. y Yohn, T. L. (1996). Accounting classification and the predictive content of earnings. Accounting Review 71, 337-355
- Fabris, T. R. y da Costa Jr, N. C. A. (2010). Propriedades das series temporais dos lucros trimestrais das empresas brasileiras negociadas em bolsa. Revista Brasileira de Finanças, 8(3), pp. 351-376.
- Fama, E. F. y French, K.R. (2000). Forecasting Profitability and Earnings. The Journal of Business 73, pp. 161-175.
- Farfield, P.M. y Yohn T.L. (2001). Using asset turnover and profit margin to forecast changes in profitability. Review of Accounting Studies, 6, pp. 371-385.
- Fairfield, P. M., Ramnath, S. y Yohn. T. L. (2009). Do Industry‐Level Analyses Improve Forecasts of Financial Performance? Journal of Accounting Research 47,147-178.
- Freeman, R. N., Ohlson, J. A. y Penman, S. H. (1982). Book rate-of-return and prediction of earnings changes: An empirical investigation. Journal of accounting research, pp. 639-653.
- Gerakos, J. J. y Gramacy, R. (2013). Regression-based earnings forecasts. Chicago Booth Research Paper, (12-26). Disponible en https://papers.ssrn.com/sol3/papers.cfm?abstract_id= 2112137
- Hoechle, D. (2007). Robust standard errors for panel regressions with cross-sectional dependence. The stata journal, 7(3), 281-312.
- Lipe, R. y Kormendi, R. (1994). Mean Reversion in Annual Earnings and Its Implications for Security Valuation. Review of Quantitative Finance and Accounting 4, 24-46.
- Little, I.M.D. (1962). Higgledy piggledy growth. Bulletin of the Oxford Institute of Economics and Statistics, 24, pp. 389-342.
- Monahan, S. J. (2018). Financial Statement Analysis and Earnings Forecasting. Foundations and Trends® in Accounting, 12(2), pp. 105-215.
- Monterrey Mayoral, J y Sánchez Segura, A (2017). Una evaluación empírica de los métodos de predicción de la rentabilidad y su relación con las características corporativas. Revista de Contabilidad 20, 95-106.
- Mullainathan, S. y Spiess, J. (2017). Machine learning: an applied econometric approach. Journal of Economic Perspectives, 31(2), pp. 87-106.
- Mueller, D. C. (1977). The Persistence of Profits above the Norm. Economica 44, 369-380.
- Myers, S. C. (1984). The Capital Structure Puzzle. The Journal of Finance 39, pp. 575-592.
- Ohlson, J. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18, pp. 109-131.
- Ohlson, J. (1995). Earnings, book values, and dividends in equity valuation. Contemporary Accounting Research 22, pp. 661-687.
- Ou, J.A. (1990). The information content of nonearnings accounting numbers as earnings predictors. Journal of Accounting Research 28, pp. 144-163.
- Pesaran, M. H. (2004). General diagnostic tests for cross section dependence in panels. CESifo Working Paper Series No. 1229; IZA Discussion Paper No. 1240. Disponible en https: www.// ssrn.com //ssrn.com/abstract=572504
- Piotroski, J. D. (2000). Value investing: The use of historical financial statement information to separate winners from losers. Journal of Accounting Research, 38, pp. 1-52.
- Penman, S.H. y Zhang X. (2002). Modeling sustainable earnings and P/E ratios with financial statement analysis. Working paper de la Columbia University y University of California, Berkeley. Disponible en http://papers.ssrn.com/sol3 /papers.cfm? Abstra ctid =318967.
- Richardson, S., Sloan, R, Soliman, M. y Tuna, I (2005). Accrual reliability, earnings persistence, and stock prices. Journal of Accounting and Economics 39, 437–485
- Schipper, K. y Vincent. L. (2003). Earnings quality. Accounting Horizons 17 (supplement), pp. 97–110.
- Sloan, R. (1996). Do stock prices fully reflect information in accruals and cash flows about future earnings? Accounting Review 71, 289–315.
- Stigler, G. (1963). Capital and Rates of Return in Manufacturing Industries. Princeton, NJ: Princeton University Press.
- Swanson, E. P., Rees, L., & Juarez-Valdes, L. F. (2003). The contribution of fundamental analysis after a currency devaluation. The Accounting Review, 78(3), pp. 875-902.
- Terreno, D. D., Sattler, S. A., & Castro González, E. L. (2018). Capacidad predictiva de la rentabilidad en empresas del mercado de capitales de Argentina. Contaduría y administración, 63(4), pp. 1-20.
- Vorst, P. y Yohn, T. L. (2018). Life cycle models and forecasting growth and profitability. The Accounting Review, 93(6), pp. 357-381.
- Wahlen, J.M., Baginski, S.P. y Bradsaw, M.T. (2011). Financial Reporting, Financial Statement Analysis, and Valuation: A Strategic Perspective (7th Ed). Mason, USA: South-Western Cengage Learning.
- Watts, R. L. y Leftwich, R. W. (1977). The time series of annual accounting earnings. Journal of Accounting Research, pp. 253-271.
- Verbeek, M. (2000). A guide to modern econometrics. Chichester: John Wiley
BIBLIOGRAFÍA
Información del número
Revista de Investigación en Modelos Financieros
Volumen 2 - 2020
ISSN: 2250-687X
ISSN (En línea): 2250-6861